https://doi.org/10.18593/r.v47.30051

Movimento entre concreto e abstrato na formação de conceitos matemáticos por estudantes privados de liberdade

Movement between concrete and abstract in the formation of the mathematic concepts by freedom deprived students

Movimiento entre concreto y abstracto en la formación de conceptos matemáticos por estudiantes privados de libertade

Francisco Carneiro Braga1

Universidade do Sul de Santa Catarina; Professor e Pesquisador.

https://orcid.org/0000-0002-4275-8122

Josélia Euzébio da Rosa2

Universidade do Sul de Santa Catarina; Professora e Pesquisadora.

https://orcid.org/0000-0001-5738-8518

Resumo: Como ensinar matemática para estudantes privados de liberdade em tempos de pandemia? A partir deste desafio, foi proposto o objetivo de investigar o movimento do pensamento matemático de estudantes privados de liberdade, durante a formação do conhecimento referente à relação de multiplicidade. Uma pesquisa foi realizada por meio de experimento didático com quatro estudantes matriculados Educação de Jovens e Adultos, em uma cadeia pública localizada no sertão paraibano. O experimento foi planejado e executado com base nos fundamentos da Teoria do Ensino Desenvolvimental de Davídov e da Atividade Orientadora de Ensino de Moura. Por causa da pandemia, não houve contato físico com os estudantes, e a comunicação foi apenas na forma escrita. Para tanto, foi providenciado um caderno para cada estudante. As tarefas impressas eram enviadas em uma folha A4 coladas nos cadernos. Os estudantes pensavam coletivamente a solução de cada tarefa e registravam individualmente, na forma manuscrita, em seus respectivos cadernos a síntese coletiva. Portanto, a fonte de dados consiste nas respostas dos estudantes. Os resultados indicam que, apesar de os colaboradores estarem privados de liberdade, eles são capazes de aprender coletivamente, desde que o ensino seja organizado em tal direção, e sejam propiciadas as condições objetivas para sua efetivação.

Palavras-Chave: Educação matemática; Experimento didático; Conhecimento teórico.

Abstract: How do teaching mathematics to freedom deprived students in pandemic time? From this challenge, it was proposed investigate the movement of mathematical thinking of freedom deprived students during theoretical knowledge formation, regarding the multiplicity relation. Research was conducted through didactic experiment with students enrolled in the Youth and Adult Education in a public prison located in Paraíba countryside. The experiment was planned and executed based on the foundations of Development Teaching Theory by Davídov and Teaching Guiding Activity by Moura. The was no physical contact with the students because of the pandemic, and the communication was only in written form. Thereunto, a notebook was provided for each student. The tasks were printed on an A4 sheet and pasted in their notebooks. Students collectively thought about the solution of each task and individually handwritten the collective synthesis in their respective notebooks. Therefore, student responses are the data source. Results point that, despite the participants were freedom deprived, they are able to learn collectively, since the teaching is organized in that direction, and objective conditions are provided for its effectiveness.

Keywords: Mathematic education; Didactic experiment; Theorical knowledge.

Resumen: ¿Como enseñar matemática para estudiantes privados de libertad en tiempos de pandemia? Desde ese desafío, fue propuesto el objetivo de investigar el movimiento del pensamiento matemático de estudiantes privados de libertad, durante la formación del conocimiento teórico referente hacia la relación de multiplicidad. Una investigación fue realizada por medio de un experimento didáctico con estudiantes matriculados en la Educación de Jóvenes y Adultos en una cárcel pública localizada en el sertão del estado de Paraíba. El experimento fue planeado y ejecutado con base en los fundamentos de la Teoría de la Enseñanza del Desarrollo de Davídov y de la Actividad Orientadora de Enseñanza de Moura. Debido a la pandemia, no hubo contacto físico con los estudiantes, y la comunicación fue solamente de manera escrita. Para ello, un cuaderno fue providenciado para cada estudiante. Las tareas eran enviadas impresas en hoja A4 pegadas en los cuadernos. Los estudiantes pensaban colectivamente la solución de cada tarea y registraban individualmente en forma manuscrita, en sus respectivos cuadernos, la síntesis colectiva. Por consiguiente, la fuente de datos son las respuestas de los estudiantes. Los resultados apuntan que, a pesar de privados de libertad, los estudiantes son capaces de aprender colectivamente, desde que la enseñanza sea organizada en esa dirección, e sean propiciadas condiciones objetivas para su efectuación.

Palabras clave: Educación matemática; Experimento didáctico; Conocimiento teórico.

Recebido em 02 de março de 2022

Aceito em 30 de novembro de 2022

1 INTRODUÇÃO

Como organizar o ensino de matemática de modo a desencadear a aprendizagem por parte de estudantes privados de liberdade durante o período pandêmico? Este foi o problema que deu origem à presente pesquisa. O ensino na prisão já era marcado por limitações impostas pelo próprio sistema prisional, por questões de segurança (BRAGA, 2021). Com a chegada do coronavírus em território brasileiro, nós, professores do sistema prisional, fomos impedidos de ir até o presídio, como fazíamos até então, para evitar a proliferação do vírus entre os apenados. Além disso, os estudantes não tinham acesso à internet.

Diante desta realidade, propomo-nos por objetivo investigar o movimento do pensamento matemático de estudantes privados de liberdade durante a formação do conhecimento referente à relação de multiplicidade. Realizamos uma pesquisa do tipo experimental, por meio de experimento didático com quatro estudantes matriculados Educação de Jovens e Adultos em uma cadeia pública localizada no sertão paraibano.

O experimento didático foi planejado e executado com base nos fundamentos da Teoria do Ensino Desenvolvimental de Davídov e da Atividade Orientadora de Ensino de Moura. Por causa da pandemia, não tivemos contato físico com os estudantes, e a comunicação foi apenas na forma escrita. Portanto, a fonte de dados consiste nas respostas manuscritas apresentadas pelos estudantes.

2 ARCABOUÇO TEÓRICO

O conhecimento, de modo geral, consiste na unidade entre abstrações, generalizações e formação de conceitos. “O movimento do sensorial-concreto ao concreto através do abstrato no pensamento, é a lei universal do desenvolvimento do conhecimento humano” (KOPNIN, 1978, p. 163). Concreto e abstrato são categorias importantes, tanto para a lógica formal tradicional quanto para a lógica dialética, tanto para formar conhecimentos empíricos quanto científicos. O pensamento que se realiza por abstrações e generalizações lógico-formais leva à formação dos conceitos empíricos. Em superação à lógica formal, o pensamento que se realiza com ajuda das abstrações e generalizações sustentadas na lógica dialética favorece a formação dos conceitos científicos (VENENCIANO et al., 2021).

De acordo com Davídov (1988, p. 100), “as particularidades da generalização, em unidade com os processos de abstração e formação de conceitos, caracterizam [...] o tipo geral de pensamento humano”. O pensamento que se realiza por meio de abstrações substanciais, generalizações substâncias e conceitos científicos é o teórico. A tarefa do pensamento teórico consiste em apreender toda representação em movimento. Aqui, os dados sensoriais somente são importantes se forem considerados em desenvolvimento. Portanto, o pensamento teórico supera o pensamento empírico, uma vez que este último se limita às propriedades externas dos objetos, e toma a aparência por essência.

Por outro lado, na formação dos conceitos teóricos, “cabe enorme papel à análise enquanto movimento que parte do concreto, dado nas sensações, ao abstrato, cabendo também à síntese enquanto movimento do abstrato a um novo concreto, que é o conjunto das definições abstratas” (KOPNIN, 1978, p. 191).

O concreto é ponto de partida e ponto de chegada do conhecimento. No início, o concreto real aparece “como o que é dado sensorialmente” (DAVÍDOV, 1988, p. 142). A atividade sensorial, nas formas de contemplação e representação, “é capaz de captar a totalidade do objeto, a presença, nele, de conexões que no processo de conhecimento conduzem à universalidade. Mas a contemplação e a representação não podem estabelecer o caráter interno destas conexões” (DAVÍDOV, 1988, p. 142).

No pensamento teórico, a passagem do sensorial concreto ao abstrato não nos afasta do mundo concreto; ao contrário: ela nos cerca dele no sentido que passamos a conhecê-lo mais profundamente, em sua essência. Só a revelação da essência dos fenômenos por meio de abstrações possibilita conhecermos o que eles têm de concreto.

Mas como conduzir, no ensino, os movimentos de redução e ascensão e favorecer a formação do pensamento teórico nos estudantes? Para investigar a formação do pensamento teórico dos estudantes, Davídov e Elkonin, ao final da década de 1950, na União Soviética, lideraram o processo de sistematização da Teoria do Ensino Desenvolvimental (DAVÍDOV, 1988). No Brasil, na década de 1990, o professor Manoel Oriosvaldo de Moura e colaboradores sistematizaram a Atividade Orientadora de Ensino.

Tanto no contexto da Teoria do Ensino Desenvolvimental quanto na Atividade Orientadora de Ensino são propostas possibilidades de superação aos diferentes modos de organização de ensino sustentados na lógica formal tradicional, que ignoram ou subestimam o lugar do sujeito e seu desenvolvimento, focando a transmissão de conteúdos prontos.

O conteúdo da Atividade de Estudo é conhecimento teórico. Nesta perspectiva, o ensino visa à potencialização máxima da capacidade de cada estudante, de modo que seu pensamento individual represente o funcionamento da atividade historicamente estabelecida a partir do desenvolvimento de tarefas de estudo.

Durante o desenvolvimento de cada tarefa de estudo, os estudantes desenvolvem ações de estudo que foram inerentes ao processo real de criação e desenvolvimento dos conceitos. Tais ações reproduzem, de forma abreviada, a unidade do lógico e do histórico no desenvolvimento da cultura humana. A tarefa de estudo é desenvolvida por meio das quatro ações de estudos em torno da essência do conhecimento teórico, com o auxílio das ações de controle e avaliação, que são: 1) revelação dos dados que compõem a relação essencial; 2) modelação da relação entre os elementos que compõem a essência; 3) transformação do modelo da relação essencial para o estudo de suas propriedades; 4) construção de um sistema de tarefas particulares; 5) controle da realização das ações de estudo; 6) avaliação da assimilação do procedimento geral de solução (DAVÍDOV, 1988).

Cada ação de estudo é desenvolvida por meio da realização de um sistema de tarefas particulares. Tomamos como tarefa de estudo a introdução dos estudantes na esfera da relação entre grandezas: formação da compreensão sobre a relação de multiplicidade. Ela foi desenvolvida por meio de uma Situação Desencadeadora de Aprendizagem. Durante a resolução do problema desencadeador, percorremos as quatro ações de estudo davidovianas, nos caminhos de redução do concreto ao abstrato (primeira e segunda ações) e ascensão do abstrato ao concreto (terceira e quarta ações).

Tanto a Teoria do Ensino Desenvolvimental quanto a Atividade Orientadora de Ensino têm por objetivo criar condições para que os sujeitos entrem em atividade de estudo e, portanto, possam se apropriar de conceitos considerados socialmente relevantes em nível teórico.

Uma das possibilidades de desencadear a aprendizagem à luz da Atividade Orientadora de Ensino consiste na história virtual do conceito. “É virtual porque contém problemas semelhantes àqueles vividos historicamente pelos seres humanos em suas lidas incessantes, em busca do aprimoramento dos meios de trabalho ou de compreensão dos fenômenos da natureza” (MOURA; ARAUJO; SERRÃO, 2019, p. 423).

O essencial, na história virtual do conceito, é a possibilidade de reconstituição do movimento de geração e desenvolvimento dos conhecimentos. Em outras palavras, o processo histórico real de geração e desenvolvimento dos conhecimentos é reconstituído virtualmente no contexto da Situação Desencadeadora de Aprendizagem do tipo História Virtual do Conceito. O problema desencadeador da História Virtual do Conceito possibilita a realização do procedimento de redução do concreto ao abstrato e ascensão do abstrato ao concreto, no processo de formação do conhecimento, por meio dos processos de abstração, generalização e formação de conceito.

3 DO ARCABOUÇO TEÓRICO À ELABORAÇÃO DO EXPERIMENTO DIDÁTICO

Com o intuito de desencadear a aprendizagem por parte de estudantes privados de liberdade durante o período pandêmico, optamos, como elemento metodológico, pela História Virtual do Conceito no contexto da tarefa de estudo.

O núcleo em torno do qual conduzimos os processos de abstração, generalização e formação de conceito consistiu na relação de multiplicidade, na unidade das significações aritméticas, geométricas e algébricas. Esse núcleo possibilitou que desvendássemos as conexões internas da tabuada, que desencadeiam a constituição de um sistema que envolve os seguintes conceitos: a) no campo aritmético – número, multiplicação, adição, divisão; b) no campo algébrico – variável, incógnita, equação e função; e c) no campo geométrico – linha reta, ponto, segmento, reta numérica, arcos.

Trata-se de uma situação elaborada para desencadear a aprendizagem de vários conceitos e, portanto, não está delimitada para um ano escolar específico. Pode ser desenvolvida nos Anos iniciais do Ensino Fundamental para desencadear a aprendizagem dos conceitos de número, multiplicação, adição, divisão e equação; em meados do Ensino Fundamental com razão, proporção, equação; Anos Finais do Ensino Fundamental com função, entre outros. Na especificidade da presente pesquisa, consideramos à relação de multiplicidade.

Ao elaborar o enredo da História Virtual do Conceito3, optamos por sujeitos fictícios, aos quais denominamos João e Antônio. O enredo foi inspirado na Lei de Execução Penal – LEP (BRASIL, 1984) e no movimento de geração e desenvolvimento da tabuada a partir das grandezas. Posteriormente, sistematizamos as tarefas particulares correspondentes a cada uma das ações de estudo. Na sequência, desenvolvemos essas tarefas com estudantes privados de liberdade, em uma cadeia pública brasileira localizada no sertão paraibano, por meio de um experimento didático desenvolvimental. Tanto o diretor da cadeia quanto a gestora da escola da rede estadual na qual os estudantes estão matriculados autorizaram a realização do experimento.

Quatro estudantes aceitaram participar da pesquisa. Destacamos que não foram escolhidos pelo pesquisador: a participação ou não na pesquisa era uma opção dos estudantes matriculados. Para preservar suas identidades, solicitamos que escolhessem um nome fictício na ocasião da assinatura do Termo de Consentimento Livre e Esclarecido – TCLE. João Victor (27 anos), Rafael (23 anos), Daniel (32 anos) e Caik (37 anos) são os pseudônimos por eles apresentados. Os estudantes colaboradores da pesquisa tinham recém-concluído o quinto, oitavo e nono ano do Ensino Fundamental, e primeiro ano do Ensino Médio, respectivamente. Todos estudam na modalidade de Educação de Jovens e Adultos – EJA no sistema prisional.

Para conduzir o processo de busca de solução para o problema desencadeador, tomamos, como ponto de partida, o procedimento geral de solução, válido não apenas para o contexto da Situação Desencadeadora que elaboramos, mas para qualquer caso do mesmo tipo. Desse modo, seguimos o movimento do geral para o particular, por meio do procedimento de redução do concreto ao abstrato e ascensão do abstrato ao concreto, conforme a Figura 1, a seguir.

Figura 1 – Movimento do processo de formação do conhecimento percorrido

Fonte: os autores (2021).

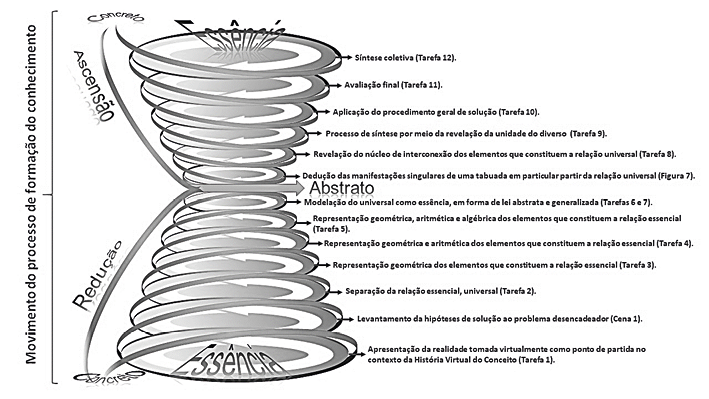
Na sequência, apresentamos e analisamos a objetivação desse movimento (Figura 1) na organização do ensino, em unidade com as manifestações dos estudantes colaboradores da presente pesquisa.

4 DESENVOLVIMENTO DO EXPERIMENTO DIDÁTICO DESENVOLVIMENTAL

Desenvolvemos o experimento didático por meio de uma tarefa de estudo a partir de uma Situação Desencadeadora de Aprendizagem, composta por quatro ações de estudo executadas por um sistema de tarefas particulares, permeadas pelas ações de controle e avaliação. Por causa da pandemia causada pelo coronavírus, SARS-CoV2, não tivemos contato físico com os estudantes. A comunicação entre professor/pesquisador e colaboradores da pesquisa foi realizada apenas na forma escrita. Para tanto, providenciamos um caderno para cada estudante. As tarefas eram impressas em uma folha A4 e coladas nos cadernos. A fonte de dados de pesquisa consiste nas respostas dos estudantes às tarefas particulares, na forma manuscrita em seus respectivos cadernos. As respostas dos estudantes refletem o caminho do pensamento pelo qual percorreram ao longo do experimento.

O experimento didático foi realizado no período de férias escolares dos colaboradores, ao longo de 19 dias, entre 8 de janeiro e 10 de fevereiro de 2021. Era imprescindível concluir o experimento no dia 10 de fevereiro, pois no dia seguinte o diretor entraria em férias, e só permitiu a realização da pesquisa nos momentos em que ele estivesse presente no local.

Todos os dias, às 8h, de segunda a sexta-feira, levávamos as tarefas, e no mesmo dia, às 16h, buscávamos. Não houve contato com os estudantes, conforme já mencionado. O diretor da cadeia indicou uma pessoa responsável por receber e entregar os cadernos diariamente. A partir das respostas devolvidas pelos estudantes, elaborávamos a próxima tarefa a ser enviada no dia seguinte. Assim, realizamos a avaliação do processo de formação do conhecimento por parte dos estudantes durante todo o processo por meio da ação de avaliação.

Sugerimos aos colaboradores da pesquisa que as reflexões sobre a solução de cada tarefa particular fossem realizadas coletivamente, pois além de compartilharem a mesma cela, tomavam banho de sol em horário idêntico. No entanto, solicitamos que nos respondessem individualmente, em seus respectivos cadernos, a síntese coletiva, conforme a compreensão individual. Durante a análise dos dados, selecionamos aquelas tarefas cujas respostas manifestam a totalidade do movimento de pensamento percorrido e que apresentavam melhor visibilidade na escrita.

4.1 PRIMEIRA AÇÃO DE ESTUDO

O ponto de partida para a formação do conhecimento teórico, ou seja, para a formação da generalização, em unidade com os processos de abstração e formação de conceito, consiste na realidade. Na especificidade da Matemática, os elementos da realidade que são reproduzidos na lógica de conceitos são as grandezas e as formas concretamente dadas.

As relações entre grandezas deram origem, historicamente, ao conceito de número, às operações com os números e, consequentemente, à tabuada (ROSA; BECKER, 2021). A primeira ação de estudo tem por finalidade revelar a relação universal que subsidia a formação do procedimento geral de solução ao problema desencadeador da Situação Desencadeadora de Aprendizagem. A relação essencial, revelada na primeira ação de estudo, atua como como base genética, como fonte do conhecimento.

Iniciamos o desenvolvimento da primeira ação de estudo com a primeira tarefa particular. Ela consistia na leitura da História Virtual do Conceito, enviada impressa em uma folha A4, colada nos cadernos (Quadro 1).

Quadro 1 - Tarefa 1 – História Virtual do Conceito

João e Antônio começaram a cumprir pena no início de 2021 em uma cadeia brasileira. Ambos foram matriculados na EJA. Porém, estão em dúvidas sobre quais benefícios essas aulas poderiam lhes trazer. A direção da escola informou-lhes que são dois benefícios importantes. Primeiro: o conhecimento escolar, quando compreendido em sua essência, possibilita que o ser humano tome consciência da estrutura social vigente, do lugar que ele ocupa na sociedade, e da necessidade de sua transformação deflagrada pelas camadas sociais menos favorecidas. Segundo: além do conhecimento a ser adquirido durante as aulas, cada três dias de aula equivalem a um dia a menos de pena. João e Antônio consideraram de extrema importância a possibilidade de serem corresponsáveis pelo projeto de transformação da sociedade, e queriam começar ali mesmo, durante o cumprimento da pena. Por esta razão, decidiram frequentar as aulas. Além disso, questionaram-se: se cada três dias de aulas equivale um dia a menos de pena, quantos dias a menos de pena teremos se assistirmos a todas as aulas? Porém, João e Antônio não sabem como fazer esse cálculo. Escreva uma carta aos dois amigos, explicando-lhes como se faz para calcular quantos dias a menos de pena terão por assistirem às aulas.

Fonte: os autores (2021).

A História Virtual do Conceito é finalizada com a solicitação da escrita de uma carta-resposta. Diante dos limites de comunicação com os estudantes, contemplamos, de forma mais explícita no enredo, os dados do problema: cada três dias de aulas equivalem a um dia a menos de pena. Essa informação poderia estar oculta e ser levantada junto aos estudantes, se a comunicação fosse realizada em tempo real, ou se tivéssemos mais tempo para desenvolver o experimento. A opção pela carta-resposta também ocorreu em função da forma de comunicação utilizada.

O problema desencadeador, que consistia em fio condutor das reflexões e que estava implícito na solicitação da escrita da carta-resposta, era: como João e Antônio podem proceder para calcular quantos dias a menos de pena terão por assistirem às aulas?

A resolução de um problema desencadeador em nível teórico implica a revelação da relação geneticamente inicial do procedimento geral de solução, a partir da relação entre grandezas (dias de aulas assistidos e dias de remissão na pena). Ao mesmo tempo, também implica a revelação de como essa relação se manifesta na solução do problema, independentemente do número singular de aulas assistidas.

Esse é um momento primordial no desenvolvimento do experimento, pois só será possível desencadear o processo de formação do conhecimento se a necessidade humana subjacente ao problema desencadeador for compreendida (ROSA; BECKER, 2021). Em outras palavras, a compreensão do problema desencadeador passa pela compreensão da necessidade dos personagens e da revelação da relação entre grandezas que subsidia sua satisfação.

Para levantar algumas hipóteses de solução, solicitamos aos estudantes que respondessem à carta aos personagens da História Virtual. As hipóteses possibilitaram que averiguássemos o estágio inicial de desenvolvimento dos estudantes em relação à formação do procedimento geral de solução do problema desencadeador e, consequentemente, determinássemos o caminho a ser percorrido nas tarefas seguintes. Nesse primeiro momento, as respostas expressaram diferentes níveis de formação.

Quadro 2- Primeira carta-resposta

João Victor: Bom dia, João e Antônio, para saber quantos dias a menos de pena teremos se assistirmos a todas as aulas, eu preciso ter mais informações. Rafael: Oi, amigos João e Antônio. A princípio acho que esse seu problema vai ajudar muitos de nós quando resolvido, pois é uma dúvida que todos nós temos diariamente. Acho que vocês podem multiplicar o número de dias de aulas pelo desconto que vão conseguir ao assistir a essas aulas. Espero ter ajudado. Quando souber a resposta, avise. Daniel: Bom dia, João e Antônio. Para ajudá-los a resolver essa situação sugiro que vocês pensem as seguintes coisas: o número de dias de aula assistidos tem uma relação direta com o desconto de dias na pena, acho que com esses dados vocês conseguirão chegar ao cálculo ou à maneira que seja válida para todos. Atenciosamente! Daniel. Caik: Bom dia, João e Antônio. Esse seu problema é nosso também, acredito que sabendo o número de aulas dá para solucionar o problema.

Fonte: Acervo do TedMat (2021).

As respostas correspondentes à primeira carta-resposta expressam o conhecimento que os estudantes formaram espontaneamente sobre o problema vivenciado em seu cotidiano. Por outro lado, a compreensão teórica do procedimento geral de solução ao problema desencadeador, do ponto de vista da Matemática, passa pela revelação da essência da tabuada. A fim de orientar o pensamento dos estudantes em direção à identificação dos elementos que compõem o procedimento geral de solução que dão origem à essência, enviamos a Tarefa 2.

Quadro 3 - Tarefa 2 – Separação da relação essencial (relação universal)

Quais informações serão necessárias para o cálculo do desconto que João e Antônio obterão na pena ao assistirem às aulas?

Fonte: os autores (2021).

No retorno à tarefa 2, os estudantes responderam que seria a relação entre a quantidade de dias de aulas assistidos em relação à quantidade de dias de remissão da pena. Portanto, apresentaram os elementos que compõem o núcleo do procedimento geral de solução. Contudo, isso não é suficiente. Faz-se necessário revelar “as passagens, o movimento, o desenvolvimento, graças ao quais se podem examinar as coisas de acordo com a sua própria natureza. Aqui incide a verdadeira significação do pensamento dialético para a ciência” (DAVÍDOV, 1988, p. 108).

Afinal, em que consiste, de fato, a relação entre os elementos revelados pelos estudantes? Quais passagens seriam possíveis? Como eles estão internamente conectados? Trata-se de uma relação fixa, ou pode ser colocada em movimento? Estas questões nortearam o modo de organização do ensino.

4.2 SEGUNDA AÇÃO DE ESTUDO

Do mundo real, extraímos os elementos da relação essencial a ser modelada na segunda ação de estudo. No processo de modelação ocorrem sucessivas abstrações, inicialmente na forma gráfica e depois na forma literal. A modelação gráfica está relacionada ao caráter visual. Porém, os modelos gráficos, sensorialmente dados aos órgãos dos sentidos, refletem as conexões internas do procedimento geral de solução do problema desencadeador. Somente após a modelação gráfica é que se atinge a modelação literal.

Os modelos na forma gráfica, constituídos por segmentos, arcos, retas, entre outros, são elementos mediadores entre o mundo real e a abstração literal. É importante ressaltar que nosso objetivo de ensino não era que os estudantes aprendessem a resolver o problema da redução de pena, mas desencadear o processo de formação do conhecimento matemático referente à relação de multiplicidade, em nível teórico, a partir do referido problema. Nesse sentido, prosseguimos em direção ao processo de abstração.

Os modelos gráficos e literais representam a relação essencial destacada na primeira ação de estudo. Mas como conduzir esse processo de abstração a distância? Como introduzir os modelos gráficos e literal a distância? Deveríamos enviar os modelos prontos e explicar seu significado? Realizar o movimento de construção com os estudantes? E quanto ao tempo? Seria possível reconstituir o movimento lógico-histórico subjacente às ações de estudo davidovianas nos poucos dias que tínhamos disponíveis? Vale lembrar que o único meio de comunicação que para subsidiar o processo de modelação era a forma escrita. Como a introdução das significações geométricas, algébricas e aritméticas subsidiaria o processo de modelação da relação essencial? Iniciamos com a introdução de elementos geométricos, como linha reta, ponto e segmento de reta na terceira tarefa (Figura 2).

Figura 2 – Introdução das significações geométricas

Fonte: Acervo do TedMat (2021).

Na tarefa anterior (Figura 2) constam as respostas do estudante Rafael, a título de ilustração das demais respostas referentes à introdução do contexto geométrico do conceito de número e da noção de infinito. De posse da introdução do contexto matemático do conceito de número, fazia-se necessária a inclusão, na quarta tarefa, da significação aritmética desse número (Figura 3).

Figura 3 – Introdução das significações aritméticas

Fonte: Acervo do TedMat (2021).

Na tarefa anterior (Figura 3), o colaborador Daniel registrou a representação dos dias de aulas assistidas, iniciando a representação a partir do zero (0), quando não havia assistido às aulas em nenhum dia; posteriormente registrou o número 1, referente a um dia de aula assistida, e assim sucessivamente, até completar o terceiro dia de aula assistida. No item D da tarefa 4 (Figura 3), por meio do arco, o colaborador representou três dias de aulas assistidas.

As respostas apresentadas por Daniel introduzem os números enquanto reflexo das relações entre objetos concretos, ou seja, dias de aulas assistidas. Neste contexto, os números não aparecem discretamente e independentes uns dos outros, mas relacionados entre si. Por exemplo, o número dois tem um lugar específico na reta numérica, antes do número três e depois do número um. O segundo dia de aula assistida começa a ser representado no ponto em que termina a representação do primeiro dia de aula: trata-se do caráter contínuo do conceito de número encarnado na reta numérica.

A tarefa em análise também propiciou o surgimento do arco, a partir da necessidade de Daniel em comunicar o total de três dias de aulas assistidas. Concomitante a criação do arco, introduzimos as significações geométricas e aritméticas. Porém, a Matemática, em seu estágio atual de desenvolvimento, passa pela indissociabilidade entre aritmética, geometria e álgebra.

O estágio mais atual de abstração em Matemática requer a modelação literal, com a introdução das letras (incógnitas e variáveis). Elas possibilitam a redução da realidade concreta à sua expressão abstrata, e subsidia a assimilação teórica do mundo. Então, como avançar no processo de abstração e revelar as significações algébricas na modalidade de ensino que estávamos desenvolvendo sem cair no método de exposição do modelo em sua forma pronta? Enfrentamos esse desafio na quinta tarefa (Figura 4).

Figura 4 – Introdução das significações algébricas

Fonte: Acervo do TedMat (2021).

Na tarefa 5 (Figura 4), Daniel revela indícios da essência da relação de multiplicidade, ao escrever que p + p + p = 3p. As demais respostas, embora com outras palavras, expressavam essa mesma essência. Como a próxima tarefa poderia dar continuidade ao movimento realizado até aqui? Em outras palavras, como reproduzir, por meio de signos, a relação essencial revelada na primeira ação de estudo?

Entendemos que o núcleo condutor de todo o processo consiste na conexão interna, na conexão entre os elementos que constituem a relação essencial. Isto porque é esta conexão que possibilita a revelação das inter-relações que geram o conhecimento em formação.

Daniel conclui a tarefa 5 (Figura 4) com a seguinte afirmação: p + p + p = 3p. Mas o que significa 3p na relação essencial em análise? Ou, explicando de outra maneira, o que significa 3p no procedimento geral de solução ao problema desencadeador em análise? A resposta para este último questionamento ocorreu na sexta tarefa (Figura 5).

Figura 5 – Abstração da interconexão dos elementos que constituem a relação essencial

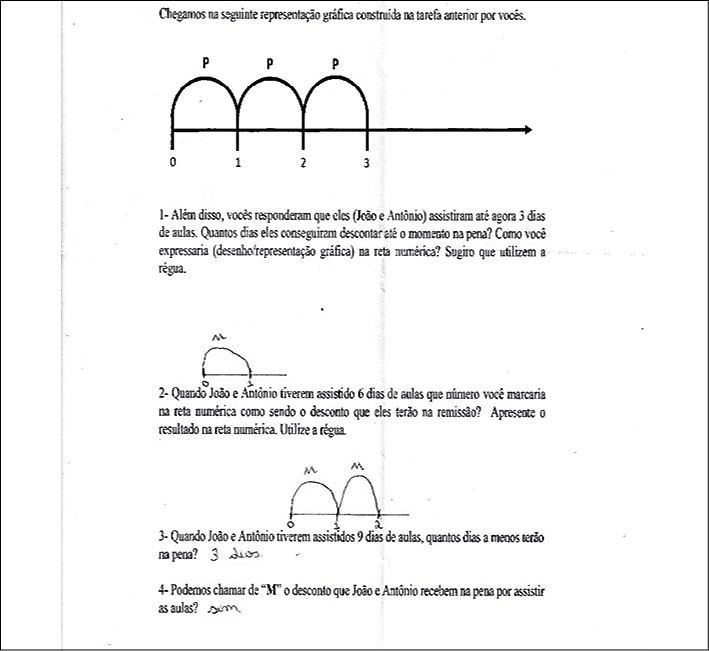
Fonte: Acervo do TedMat (2021).

A partir da sexta tarefa (Figura 5), podemos observar a representação abstrata de um dia a menos na pena (m). Isso significa que cada m representado na reta por João Victor equivale a três dias de aulas assistidas. Portanto, houve uma transição de dias de aulas assistidas (3) para a quantidade de remissão da pena a partir de interconexão dessas duas quantidades. Com base nessa mesma interconexão, na sétima tarefa foi revelado um terceiro elemento da relação geneticamente inicial (Figura 6).

Figura 6 – Abstração da interconexão dos elementos que constituem a relação essencial

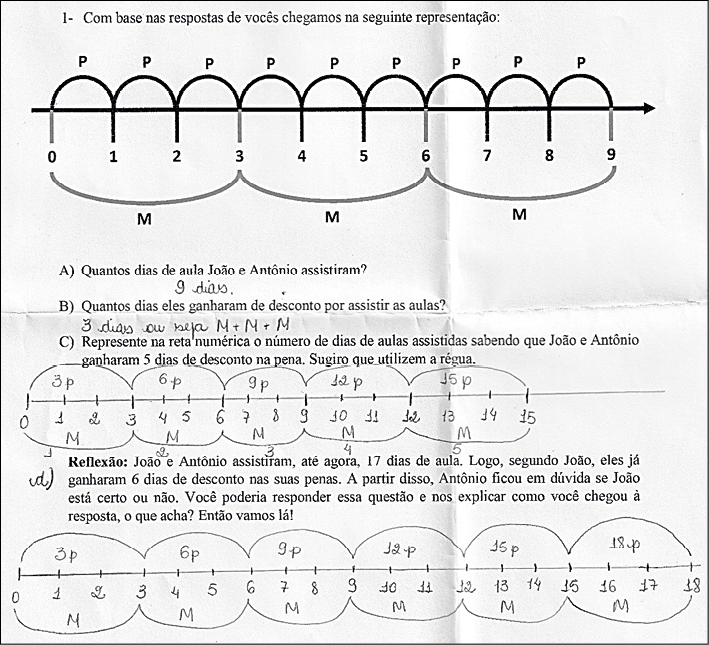
Fonte: Acervo do TedMat (2021).

No item C da tarefa 7 (Figura 6), os estudantes concluíram o processo de abstração (separação) da relação geneticamente inicial do procedimento geral de solução. Porém, nesse estágio do processo, a abstração ainda tem caráter singular: 3 × 5 = 15. No modelo gráfico (item C, tarefa 7), os arcos acima da reta representam os agrupamentos compostos por três unidades cada (3p), e os arcos abaixo representam o número de dias de remissão da pena (m). O último número consiste no total de aulas assistidas (18).

O mesmo ocorre no item D (Figura 6). A relação singular fixada no modelo gráfico consiste em: 3 × 6 = 18. No entanto, esse item contempla a ação de controle. A principal função dessa ação é assegurar se o estudante já domina o que foi desenvolvido até então. Para tanto, propõe-se uma tarefa incorreta. Os estudantes, ao identificarem a causa do erro, indicam a possibilidade de continuidade no processo de formação do conhecimento (DAVÍDOV, 1988).

Ao justificar sua compreensão no item D da tarefa 7, Rafael escreveu o seguinte: “João está errado. A partir da representação acima [reta numérica], constatei que falta um dia de aulas assistidas, para assim conseguir ganhar mais um dia, para conseguir o desconto de seis dias no total”. É importante observar que Rafael recorreu à reta numérica para subsidiar sua resposta. Ele expressa, na reta numérica, as relações essenciais da realidade vivenciada por João e Antônio, e por eles também, a partir da LEP. Em outras palavras, naquele estágio de desenvolvimento do experimento, os estudantes ainda necessitavam da reta numérica como fonte sensorial de reflexo da realidade.

Assim como o pensamento empírico, o pensamento teórico “não diminui o papel e a importância das fontes sensoriais no conhecimento” (DAVÍDOV, 1988, p. 138). Contudo, diferentemente do pensamento empírico, o pensamento teórico deve apreender a representação sensorial em movimento. Esta é a essência do enfoque dialético acerca da correlação entre a representação e o pensamento na atividade cognitiva das pessoas.

Mas como sabermos se o pensamento de Rafael abarca o movimento da essência em sua totalidade, ou se está limitado ao exemplo singular abstraído no modelo gráfico (reta numérica)? Entendemos que, na continuidade de sua explicação para o item D da tarefa 7, o estudante dá indícios de que seu pensamento abarca a representação da reta numérica em movimento, e que alcança um desenvolvimento inacessível à representação, em direção ao infinito (Figura 7).

Figura 7 – Revelação do universal como essência em forma de lei

Fonte: Acervo do TedMat (2021).

Nos exemplos anteriores, a letra p representava a unidade básica (p = 1, ou seja, um dia de aula assistida). Agora (Figura 7), Rafael utilizou a letra p para representar o valor da unidade intermediária (p = 3, ou seja, 3 dias de aulas assistidas), fixada no modelo gráfico pelos arcos registrados acima da reta (três dias de aulas assistidas); m para representar o número de dias de remissão na pena e, como resultado, o total de dias de aulas assistidas. Conforme pode ser visto na terceira ação de estudo, os estudantes representaram o total (3, 6, 9 ...) com a letra t.

Assim, o modelo literal consiste em: p × m = t. Esta é a relação essencial, a base genética do procedimento geral de solução. Esse modelo abstrato expressa a conexão geneticamente inicial que está na base do concreto, como fonte, a partir do qual todo o conhecimento se origina. Trata-se de uma abstração substancial que reflete a conexão real entre dias de aula e dias de remissão da pena, dada em forma sensório-contemplativa e determinada pela LEP.

Em que momento os estudantes colaboradores da pesquisa iniciaram o processo de abstração? O processo de abstração teve início na primeira tarefa, quando enviamos a História Virtual do Conceito aos estudantes. A necessidade vivenciada pelos personagens da história é compartilhada pelos colaboradores da presente pesquisa, que é satisfazer a necessidade de saber como se faz para calcular quantos dias a menos de pena os privados de liberdade terão ao assistirem às aulas. É importante reafirmar que não se trata de dar uma resposta numérica do tipo serão tantos dias a menos. A resolução de um problema, com potencial para desencadear a aprendizagem em nível teórico, passa pela busca do procedimento geral de solução, e este coincide com o procedimento geral de construção mental dos objetos de conhecimento.

Os estudantes iniciaram o processo de abstração ao separarem a relação genética do procedimento geral de solução, na primeira carta-resposta (Tarefa 1), conforme explica Daniel: “[...] sugiro que vocês pensem as seguintes coisas: o número de dias de aula assistidas tem uma relação direta com o desconto de dias na pena. Acho que com esses dados, vocês conseguirão chegar ao cálculo ou maneira que seja válida para todos”. Na sequência, houve continuidade no processo abstrativo por meio de abstrações sucessivas.

No início da segunda ação, os estudantes fixaram a relação essencial, inicialmente na forma singular, por meio de elementos geométricos, aritméticos e algébricos, e finalmente, na forma generalizada (p × m = t). Portanto, generalizaram a abstração substancial.

Abstração e generalização são dois aspectos do processo de análise. A redução das abstrações singulares (3 × 5 = 15 e 3 × 6 = 18) a uma única expressão, abreviada, abstrata, de caráter universal (p × m = t), foi realizada por meio da generalização substancial, na qual o “universal como essência aparece em forma de lei” (DAVÍDOV, 1988, p. 147).

Na tarefa 7, finalizamos o processo de redução dos tipos singulares de situações vivenciadas por João e Antônio à forma universal do procedimento geral de solução. O modelo p × m = t fixa o universal como essência em forma de lei.

Durante o processo de análise de situações particulares vivenciadas pelos personagens da História Virtual do Conceito, o estudante chegou à abstração por meio da separação da relação de caráter universal, da base genética do procedimento geral de solução.

Portanto, há indícios que Rafael, juntamente com seus colegas, realizou uma análise teórica que culminou com a abstração e a generalização do tipo substancial. A tarefa fundamental da análise, de acordo com a lógica dialética, consiste “na redução das diferenças existentes dentro do todo à base única que as gera, a sua essência” (DAVÍDOV, 1988, p. 147).

Por meio da reta numérica, Rafael e seus colegas realizaram a abstração da relação essencial na forma singular. Essa modelação gráfica se constituiu em meio para que os estudantes atingissem a abstração máxima por meio de letras. A reta numérica, enquanto modelação visual, reflete as vinculações internas dos elementos que constituem a relação essencial, extraídas da realidade: unidade de medida intermediária (p), quantidade de vezes que a unidade de medida intermediária se repete (m), e total de unidades básicas (t). As letras p, m e t refletem, de forma abstrata e geral, a relação abstraída (separada) do concreto real ponto de partida (relação da quantidade de dias de aulas assistidas com a de dias de remissão na pena). A relação universal p × m = t fixa a relação real entre dias de aulas assistidas e dias de remissão na pena.

A redução dos diversos fenômenos à sua base única ocorre por meio dos processos de abstração e generalização. Neste momento é importante questionar: com os processos de abstração e generalização, concluímos a formação do conceito? Ainda não. “Se o pensamento se encerra em abstrações, deixa de ser meio de conhecimento da realidade, transformando-se em instrumento para distanciar-se dela” (KOPNIN, 1978, p. 157).

De acordo com Davídov (1988, p. 214), no ensino, geralmente “o aparecimento do material abstrato (em particular os signos expressos por letras) é vinculado à finalização da aprendizagem de algum tema”. Porém, quando “o material abstrato é introduzido relativamente cedo, serve como meio para que os alunos captem os fundamentos da ação objetal” (DAVÍDOV, 1988, p. 214). Além disso, constituem-se em elemento de mediação entre o concreto real ponto de partida e a reprodução do concreto no pensamento enquanto ponto de chegada.

A redução do concreto ao abstrato é um momento subordinado, como meio para alcançar a ascensão. Na redução, por meio da análise, separam-se as abstrações indispensáveis para o posterior movimento do pensamento em direção ao concreto por meio da dedução. “Na dedução revelamos, mostramos como, por que e em que base dado singular está relacionado com esse universal” (KOPNIN, 1978, p. 157). O conceito científico “serve de procedimento para deduzir os fenômenos particulares e singulares de sua base universal” (DAVÍDOV, 1988, p. 152). O universal “corresponde às possibilidades potenciais de base genética de certo todo” (DAVÍDOV, 1988, p. 145).

O conceito científico possui conteúdo e forma. Por seu conteúdo, “o conceito científico aparece com reflexo dos processos de desenvolvimento, da relação entre o universal e o singular, da essência e os fenômenos” (DAVÍDOV, 1988, p. 152). Por sua forma, o conceito científico “aparece como procedimento da dedução do singular a partir do universal, como procedimento de ascensão do abstrato ao concreto” (DAVÍDOV, 1988, p. 152).

Até o presente momento, analisamos os procedimentos de abstração e generalização; na sequência, passamos a analisar o procedimento de formação do conceito.

4.3 TERCEIRA AÇÃO DE ESTUDO

De acordo com a lógica dialética, o desenvolvimento do pensamento teórico segue o “movimento de conhecimento desde o concreto ao abstrato e do abstrato ao concreto” (ILIENKOV, 2006, p. 189). Desse modo, na terceira e quarta ações ocorre a concretização do conhecimento teórico por meio da dedução e explicação das manifestações particulares e singulares do sistema integral, a partir do fundamento universal já abstraído e generalizado.

No item D da tarefa 7 (Figura 7), ao explicar o equívoco de um dos personagens, Rafael atingiu a abstração máxima (p × m = t), válida para qualquer tabuada particular (neste caso, a tabuada do número três, mas poderia ser outra, a depender do valor atribuído à variável p) e suas manifestações singulares (3 × 1 = 3; 3 × 2 = 6;...). Cada relação singular (3 × 1 = 3...) corresponde a uma situação específica, que pode ser vivenciada por um detento, na relação entre dias de estudo e dias de remissão da pena. O caso particular da lei atual de remissão de pena consiste na tabuada do número três. Mas se a lei mudar e para cada quatro dias de aulas assistidas equivaler um dia a menos de remissão na pena, a relação geneticamente inicial será a mesma, só que em vez de p = 3, será p = 4. A relação (p × m = t) é universal para o conceito de tabuada. “O universal implica a riqueza do singular e do particular no sentido de que, apreendendo as leis, ele está refletindo, nessa ou naquela medida, todos os casos particulares de manifestação do singular” (KOPNIN, 1978, p. 108).

Rafael iniciou o processo de dedução do concreto de forma autônoma, ao tentar explicar o modelo que ele mesmo elaborou em forma de lei (Figura 7). Logo abaixo do modelo, Rafael revelou a vinculação regular da relação essencial com suas diferentes manifestações singulares, o que culminou com a sistematização de uma tabuada particular, a do número três, em direção ao infinito. Esta mesma relação (p × m = t) dá origem a todas as tabuadas particulares. Para p = 2, a tabuada do número dois; para p = 5, a tabuada do número cinco; e assim sucessivamente.

A essência, quando abstraída e generalizada em nível teórico, constitui-se em fonte, base genética para a dedução de manifestações particulares e singulares. A relação p × m = t é a unidade das diversas manifestações da relação de multiplicidade. “A reprodução teórica do concreto real como unidade do diverso se realiza pelo procedimento de ascensão do abstrato ao concreto” (DAVÍDOV, 1988, p. 141). Poderíamos, a partir desse estágio de desenvolvimento, dar continuidade em direção à formação do conceito de função. Entretanto, diante dos limites de tempo, iniciamos o processo de redução.

No processo de dedução do concreto a partir do abstrato é necessário revelar o elo que interconecta os elementos que constituem a relação universal. Se são conhecidos dois dos três valores que constituem o modelo da relação universal (p × m = t), o terceiro pode ser determinado por meio da transformação do modelo (t ÷ p = m e t ÷ m = p). Há um núcleo comum entre as três relações, conforme revela Rafael, na resolução da tarefa 8 (Figura 8).

Figura 8 – Revelação do núcleo de interconexão dos elementos da relação universal

Fonte: Acervo do TedMat (2021).

No movimento em análise, a relação de divisibilidade derivou da relação de multiplicidade. A transformação do modelo permitiu a revelação da interconexão de seus elementos por meio das relações de multiplicidade e divisibilidade. Assim, por meio da transformação do modelo, é possível analisar as interconexões dos elementos que constituem o modelo universal.

Nas dependências do pensamento teórico, o estudante adentra a relação interna, revela as inter-relações, e gera um sistema de formações. Na lógica dialética, “essa integridade objetiva existente por meio das coisas singulares se chama de concreto” (DAVÍDOV, 1988, p. 130). O conteúdo do conceito científico está nos “[...] processos de desenvolvimento dos sistemas integrais” (DAVÍDOV, 1988, p. 152). Enquanto a generalização consiste na redução, o conceito científico equivale à dedução. Por isso o resultado da redução precisa assegurar a dedução; ou seja, ele deve ser a forma inicial do conceito. A forma final do conceito é “a síntese das mais diversas ideias, o resultado de um longo processo de conhecimento” (KOPNIN, 1978, p. 191). Nas respostas dos estudantes, detectamos alguns indícios do processo de síntese, conforme ocorre na tarefa 9 (Figura 9).

Figura 9 – Processo de síntese por meio da revelação da unidade do diverso

Fonte: Acervo do TedMat (2021).

Na tarefa anterior, Caik confundiu o símbolo de porcentagem com o de divisão (÷), mas as transformações por ele realizadas estão corretas. Expressar um objeto em forma de conceito significa compreender sua essência como fundamento genético, pois o conceito é reflexo da essência, e esta, por sua vez, é reflexo da realidade. A peculiaridade do conceito enquanto forma de reflexo da realidade reside na universalidade expressa abstratamente na forma algébrica. Caik afirma que “a fórmula p × m = t resolve qualquer caso do tipo” (Figura 9).

Na afirmação anterior, Caik indica ter atingido o concreto como unidade de diversas manifestações. “O concreto é concreto porque é a síntese de muitas definições, logo, a unidade do diverso” (KOPNIN, 1978, p. 162). Caik também indica ter compreendido o procedimento geral de solução, pois capta o universal como base de manifestações particulares e singulares, ou seja, como base de todas as manifestações do concreto.

O concreto ponto de chegada aparece no pensamento como processo de síntese, como resultado. Dentre os diversos casos particulares de manifestação do singular, isto é, dentre as diversas possibilidades de aplicação prática do universal, retomamos o problema desencadeador inicial para verificar a veracidade da formação do conhecimento realizada ao longo do processo.

4.4 QUARTA AÇÃO DE ESTUDO

A partir do momento em que os estudantes formaram o procedimento geral de solução da tarefa de estudo, propusemos a aplicação para solucionar o problema desencadeador. Como nos ensina Kopnin (1978, p. 153), “por força de sua universalidade e concreticidade, o conhecimento científico tem um campo irrestrito de aplicação prática”. Entretanto, como nosso tempo estava se esgotando, desenvolvemos apenas uma tarefa correspondente à quarta ação de estudo. Ela consistiu na elaboração de uma nova carta-resposta aos personagens João e Antônio. Dada a semelhança das cartas, apresentamos, a título de ilustração, a escrita por Caik.

Quadro 4 - Tarefa 10 - Segunda carta-resposta

Bom dia, João e Antônio, durante o estudo das tarefas encontramos a seguinte fórmula: P X M = T, onde: P são os dias de estudo M é o número de dia descontado na pena T é o número total de dias estudados Com essas informações e essa fórmula vocês conseguirão resolver o problema.

Fonte: Acervo do TedMat (2021).

A resposta dos demais colaboradores foi semelhante à de Caik, mas Daniel incluiu a seguinte observação: “Pode ser qualquer letra”. Nesta segunda versão da carta, os estudantes aplicaram o procedimento geral de solução. O ponto de partida e o ponto de chegada foram os mesmos, mas as repostas foram diferentes.

Na primeira carta, as respostas expressavam níveis de desenvolvimento distintos. O desenvolvimento das tarefas seguintes foi realizado em colaboração coletiva, tal como sugerem Moura, Araújo e Serrão (2019). As respostas, embora aparentemente diferentes, eram semelhantes em sua essência, uma vez que cada estudante expressava a sua compreensão individual com base nas reflexões realizadas coletivamente.

Se os estudantes soubessem fazer sozinhos, não necessitassem da colaboração dos colegas, o experimento didático não seria desenvolvimental, ou seja, não geraria desenvolvimento. De acordo com Vigotski (2001), a aprendizagem só é boa quando está na frente do desenvolvimento e o conduz. “O ensino seria totalmente desnecessário se pudesse utilizar apenas o que já está maduro no desenvolvimento, se ele mesmo não fosse fonte de desenvolvimento e surgimento do novo” (VIGOTSKI, 2001, p. 334).

Assim, questionamos: a colaboração entre estudantes é suficiente para conduzir o processo de formação do conhecimento? O trabalho do professor é dispensável? Afinal, qual foi a função enquanto professor pesquisador? Mesmo a distância, entendemos que conduzimos todo o processo de formação do conhecimento. Por meio da avaliação de cada resposta que recebíamos (ação de avaliação), elaborávamos a próxima tarefa a ser enviada no dia seguinte, a fim de orientar o pensamento dos estudantes em direção ao nosso objetivo final: a formação do procedimento geral de solução da tarefa de estudo/problema desencadeador. Cada nova tarefa, no contexto das ações de estudo, não era completamente nova: era continuidade da tarefa realizada no dia anterior. Portanto, a formação do conhecimento referente à relação de multiplicidade ocorreu no processo de aprendizagem em colaboração com os colegas e o professor pesquisador, mesmo que a distância. Mas como será que os estudantes avaliam esse modo de organização de ensino? Em busca por respostas, enviamos um questionário e solicitamos que pensassem individualmente cada questão. Eis o retorno (Tarefa 11).

Quadro 5 - Tarefa 11 – Avaliação final

Questão 1: Você aprendeu algo novo com esta pesquisa? O quê? Caik: O conhecimento é uma construção e sempre existem novas maneiras de estudar e aprender. Daniel: Sim, uma nova forma de olhar a tabuada e também de saber a redução de pena. João Victor: Aprendi a calcular os dias de desconto na pena, coisa que eu não sabia. Rafael: Sim, que o conhecimento é uma construção diária e também novas maneiras de estudar. Questão 2: Você já havia estudado multiplicação? Se sim, como foi esse estudo? Caik: Sim, com a tabuada, mas sem considerar a sua construção, agora já sei. Daniel: Sim, mais do jeito tradicional de estudar a tabuada, aqui é detalhado e bem lento o processo [sic] João Victor: Sim, mas era bem simples, a tabuada. Rafael: Sim, com a tabuada, bem simples e sem contexto. Questão 3: Prefere estudar do modo como foram essas tarefas ou como era nos anos anteriores? Caik: Desse jeito é melhor, pois entendo o passo a passo e como é construído. Daniel: Prefiro como os anos anteriores porque é direto os cálculos. [sic] João Victor: Gostei desse jeito, só que é mais difícil pois envolvem muitas coisas. [sic] Rafael: Tanto faz, só que esse é mais detalhado. Questão 4: Quais as principais dificuldades encontradas no processo de aprendizagem na prisão? Caik: Ausência de livros, as normas são diferentes e o pouco tempo em salas de aulas. Daniel: Restrição no material para estudo, carga horária baixa, a falta de atuação da equipe gestora para os presos. João Victor: Falta de livros, as regras e problemas internos também afetam na aprendizagem. Na pandemia, a falta de contato com os professores também dificulta muito. Rafael: O pouco tempo com o professor em sala de aula, às vezes a forma de como ele ensina (professores), os problemas da própria cadeia, a falta de material (internet, livros). Questão 5: Os limites da educação no sistema prisional, apontados anteriormente, interferiram no processo de ensino-aprendizagem realizado agora nas férias? Caik: Não, só a pandemia que atrapalha um pouco. Daniel: Não muito pelo contrário não houve interferência nenhuma. João Victor: Não, não senti falta de livros, apenas do contato com o professor. Rafael: Não, só a pandemia que atrapalha.

Fonte: Acervo do TedMat (2021).

Salientamos que não adaptamos as respostas acima, elas foram apresentadas na íntegra, tal como as recebemos. Na questão 1 (Tarefa 11), Caik e Rafael ressaltam o processo de construção do conhecimento por eles vivenciado. Isto condiz com o desenvolvimento das ações de estudo previsto por Davídov (1988, p. 184), que “é como se os próprios estudantes construíssem o conceito, ainda que sob a direção sistemática do professor”. Na segunda questão, Daniel afirma que já tinha aprendido, em experiências anteriores, a tabuada do modo tradicional, e Caik complementa que foi sem considerar sua construção.

Na quarta questão, os estudantes apontaram limites na educação do sistema prisional, e na quinta afirmaram que esses limites não interferiram no desenvolvimento do experimento didático em análise. Isto nos leva a supor que não é o fato de o ensino ser desenvolvido no sistema prisional ou fora dele que limita o processo de formação do conhecimento, mas o conteúdo e o método de seu desenvolvimento, tanto no sistema prisional quanto fora dele, que requerem melhores condições para que os professores possam repensar o modo de organização de ensino vigente.

Para finalizar o experimento, solicitamos que os estudantes elaborassem, coletivamente, um título para a História de João e Antônio (Tarefa 12). Eis o título que nos enviaram: “Educação mudando vidas: da cela para a liberdade”. Desejamos que assim seja.

5 CONSIDERAÇÕES FINAIS

Investigamos o pensamento matemático de estudantes privados de liberdade durante a formação do conhecimento referente à relação de multiplicidade. Ao longo da realização do experimento didático, enfrentamos algumas questões específicas, como pouco tempo para o desenvolvimento do referido experimento, e a comunicação unicamente na forma escrita, devido à pandemia causada pelo coronavírus SARS-CoV2. Ainda assim, nas respostas dos estudantes há indícios de formação de alguns elementos da relação de multiplicidade em nível teórico, conforme indica a diferença entre a primeira e última carta-resposta. A primeira carta apresentava respostas dispersas e rasas; a última, por sua vez, apresentou evidências de superação das compreensões iniciais relacionadas ao procedimento geral de solução do problema desencadeador. Destacamos que a primeira resposta dos estudantes não estava errada, apenas empiricamente sustentada.

Os resultados indicam que, apesar de os colaboradores estarem privados de liberdade, eles são capazes de aprender coletivamente, desde que o ensino seja organizado em tal direção. Em outras palavras, entendemos que o problema não está no estudante, mas no modo de organização do ensino e nas condições objetivas para sua efetivação.

Uma das limitações de nossa experiência investigativa incide na impossibilidade do contato presencial por conta da pandemia. Acreditamos que os resultados dos processos de ensino e aprendizagem poderiam ter sido potencializados, caso fossem desenvolvidos na presencialidade. Não tivemos esta possibilidade por conta dos limites da grandeza tempo disponível para a conclusão da pesquisa. Portanto, deixamos essa temática como sugestão para futuras investigações.

REFERÊNCIAS

BRAGA, F. C. Movimento do pensamento matemático em nível teórico a partir da relação de multiplicidade por estudantes privados de liberdade. 2021. 101 f. Dissertação (Mestrado em Educação) - Universidade do Sul de Santa Catarina, Tubarão, 2021.

BRASIL, Lei de Execução Penal nº 7.210, de 11 de julho de 1984. Institui a Lei de Execução Penal. Diário Oficial da União: Brasília, DF, p. 10227, 13 jul. 1984. Disponível em: http://www.planalto.gov.br/ccivil_03/Leis/L7210.htm. Acesso em: ago. 2020.

DAVÍDOV, V. V. La enseñanza escolar y el desarrollo psíquico: investigación psicológica teórica y experimental. Tradução Marta Shuare. Moscou-Rússia: Editorial Progreso, 1988.

ILIENKOV, E. V. La ascensión de lo abstracto a lo concreto en principios de la lógica dialéctica. In: JIMÉNES, A. T. Teoría de la construcción del objeto de estudio. México: Instituto Politécnico Nacional, p. 151-200, 2006.

KOPNIN, P. V. A dialética como lógica e teoria do conhecimento. Rio de Janeiro: Civilização Brasileira, 1978.

MOURA, M. O.; ARAUJO, E. S.; SERRÃO, M. I. B. Atividade Orientadora de Ensino: fundamentos. Linhas Críticas, 24, 2019.

ROSA, J. E. da; BECKER, F. Desenvolvimento de uma situação desencadeadora de aprendizagem do conceito de ângulo por meio de quatro ações de estudo davidovianas em um contexto de formação inicial de professores. Obutchénie. Revista de Didática e Psicologia Pedagógica, v. 5, n. 2, p. 484-516, jun. 2021.

VENENCIANO, L. et al. An introduction to multiple perspectives on Davydov’s approach in the XXI century. Educ Stud Math, [online], n. 106, p. 323–326, 2021. DOI 10.1007/s10649-021-10040-5.

VIGOTSKI, L. S. A construção do pensamento e da linguagem. Tradução: Paulo Bezerra. São Paulo: Martins Fontes, 2001.

---