art_3_-_impacto_da

https://doi.org/10.18593/race.23798

IMPACTO DA CRISE ECONÔMICA DE 2014 A 2016 SOBRE O COEFICIENTE BETA DO MERCADO DE CAPITAIS BRASILEIRO

Impact of the 2014 to 2016 economic crisis on the beta coefficient of the Brazilian stock market

Vinícius Luís de Souza Nonato

E-mail: viniciuslsn@hotmail.com

Bacharel em Ciências Econômicas pela Universidade Católica de Brasília; Analista de Políticas e Indústria da Confederação Nacional da Indústria.

Endereço para contato: QR 412 Conjunto 1, 15, Samambaia Norte, 72320-101, Brasília, DF, Brasil.

https://orcid.org/0000-0002-8135-4411

Paula Virgínia Tófoli

E-mail: paula.tofoli@ucb.br

Doutora em Economia pela Universidade Federal do Rio Grande do Sul; Mestra em Economia pela Universidade Federal do Rio Grande do Sul; Professora no Curso de Pós-graduação em Economia da Universidade Católica de Brasília.

https://orcid.org/0000-0002-2256-1584

Artigo recebido em 12 de fevereiro de 2020. Aceito em 17 de julho de 2020.

Resumo

Estudos empíricos têm encontrado evidências de que o risco de mercado, ou beta de mercado, tende a aumentar em períodos de crise. Dada a crise econômica brasileira de 2014 a 2016, o objetivo deste artigo foi analisar se esta teve um impacto significativo sobre o risco de mercado das empresas brasileiras com ações negociadas na Brasil, Bolsa, Balcão (B3). Para isso, estimou-se a trajetória do beta de uma carteira de ações negociadas na B3 para o período de fevereiro de 2010 a dezembro de 2018, considerando um modelo CAPM condicional em que a dinâmica de beta é dada por um processo estocástico combinado com um conjunto de variáveis condicionantes relacionadas ao ciclo econômico. Encontramos evidências de que o beta da carteira teve um aumento a partir de janeiro de 2015 e somente retornou a patamares do período pré-crise a partir de março de 2018. Essas evidências estão de acordo com os resultados encontrados na literatura internacional e têm implicações importantes em termos de gerenciamento de risco.

Palavras-chave: Beta de mercado. Crise. B3. CAPM condicional. Filtro de Kalman.

Abstract

Empirical studies have found evidence that the market risk, or market beta, tends to increase in crisis periods. Given the Brazilian economic crisis from 2014 to 2016, this paper investigates whether this crisis had a significant impact on the market risk of the Brazilian firms with stocks negotiated at the Brazilian stock market, Brasil, Bolsa, Balcão (B3). For this, we estimated the trajectory of the beta of a portfolio of stocks traded on B3 for the period from February 2010 to December 2018, considering a conditional CAPM with the dynamics of beta given by a stochastic process combined with conditioning variables related to the economic cycle. We found evidence that the portfolio beta had an increase by January 2015, and only returned to values of the pre-crisis period by March 2018. This evidence is aligned with results found in the international literature and has important implications in terms of risk management.

Keywords: Market beta. Crisis. B3. Conditional CAPM. Kalman filter.

1 INTRODUÇÃO

A economia brasileira passou por uma profunda recessão entre o segundo trimestre de 2014 e o quarto trimestre de 2016, com 11 trimestres consecutivos de queda no PIB, de acordo com o Comitê de Datação de Ciclos Econômicos (Codace) da Fundação Getúlio Vargas. O PIB do último trimestre de 2016 recuou 7,9% em relação ao mesmo período de 2014, fazendo com que a economia brasileira retornasse a patamares de 2010, de acordo com dados das Contas Nacionais Trimestrais, do IBGE. A redução de 8,9% no consumo das famílias e de 23,5% no investimento foram os principais motores desse encolhimento da economia. A recessão chegou ao fim em 2017, quando a economia teve crescimento de 1%, recuperando-se a passos lentos desde então.

De acordo com Barbosa (2015), o primeiro mandato de Dilma Rousseff, com sua Nova Matriz Econômica, gerou um quadro de inflação elevada e baixo crescimento econômico. Tal matriz foi baseada em uma política fiscal expansionista, na fixação de taxas de juros baixas, incompatíveis com as metas de inflação, na intervenção do Banco Central no mercado cambial e no controle de preços de derivados do petróleo e tarifas de energia elétrica. Essa política econômica, somada às investigações da operação Lava Jato e à crise política vivida no período, resultaram, segundo Barbosa, no aumento da incerteza no cenário macroeconômico brasileiro, o que agravou a crise econômica. Isso se refletiu em grande volatilidade no mercado financeiro, de modo que o Ibovespa, principal índice da B3, caiu cerca de 40,5% entre o ponto de máximo em setembro de 2014, aos 62.305 pontos, e o ponto de mínimo em janeiro de 2016, aos 37.046 pontos.

Em cenários de crise como esse, a maior volatilidade no mercado acionário pode ser percebida pelos investidores como um aumento no risco do investimento em ações. De acordo com Chen e So (2002), quando os retornos das ações são mais voláteis, com tudo mais permanecendo constante, espera-se que o risco (beta) de mercado seja mais elevado, com maiores respostas dos preços das ações de firmas que têm maior exposição a esse tipo de risco. Assim, os investidores podem migrar para ativos menos arriscados, como os títulos. Essa reação tenderia a aumentar o custo de financiamento das firmas que emitem ações. Estudos empíricos, como os de Alexandridis e Hasan (2019), Asgharian, Christiansen, e Hou (2017), Chen e So (2002), Choudhry (2005) e Choudhry, Lu, e Peng (2010) indicam que o beta de mercado dos ativos tende a aumentar nos períodos de crise e pós-crise.

Já é considerado um fato empírico que o beta de um ativo de risco ou portfólio é variante no tempo (Fabozzi & Francis, 1978). As mudanças em beta ao longo do tempo podem ser explicadas tanto por fatores macroeconômicos (como risco do País, qualidade do ambiente de negócios, políticas fiscal e monetária, entre outros) quanto por fatores microeconômicos (como governança das empresas, níveis de produtividade e ociosidade, endividamento, entre outros). Embora o modelo Capital Asset Price Model (CAPM) ainda hoje seja o modelo de apreçamento e avaliação de risco de ativos mais utilizado na prática (Fama & French, 2004), por sua simplicidade ou por seu apelo intuitivo, um de seus maiores problemas é assumir beta constante ao longo do tempo. Para corrigir essa falha, surgiu o modelo CAPM condicional. Destacam-se duas abordagens principais do CAPM condicional: aquela em que beta é uma função determinística de variáveis condicionantes relacionadas ao ciclo econômico; e aquela em que a dinâmica de beta pode ser especificada por meio de um modelo de séries temporais. Existe, ainda, o modelo condicional híbrido, em que a dinâmica de beta é descrita por um processo estocástico combinado com variáveis condicionantes. Ver, por exemplo, Adrian e Franzoni, (2009) e Blank, Samanez, Baidya, e Aiube (2014).

O objetivo deste artigo é analisar se a crise de 2014 a 2016, que tomou conta da economia brasileira, teve um impacto significativo sobre o risco (beta) de mercado das empresas de capital aberto negociadas na bolsa de valores brasileira. Para isso, analisou-se o comportamento do beta de uma carteira composta por ações de empresas brasileiras negociadas na B3, pertencentes a setores distintos da economia, ao longo do período de fevereiro de 2010 a dezembro de 2018. Para se obter a trajetória temporal do beta da carteira selecionada, seguiu-se Blank et al. (2014), modelando a dinâmica de beta como um processo estocástico (de reversão à media ou passeio aleatório) combinado ou não com variáveis condicionantes relativas ao ciclo econômico e estimando-a por meio do Filtro de Kalman. Para efeito de comparação, também estimou-se o beta de mercado considerando o modelo CAPM incondicional.

Este estudo contribui para a literatura que trata dos efeitos de crises sobre o risco sistemático das empresas, em particular, para o caso das empresas brasileiras, para o qual os estudos são escassos. Assim como Blank et al. (2014), exploraram-se os ganhos da modelagem híbrida encontrados por Adrian e Franzoni (2009) para dados do mercado norte-americano, e adicionaram-se variáveis macroeconômicas relacionadas diretamente à economia brasileira. Os poucos artigos que tratam do comportamento do risco sistemático das empresas brasileiras em períodos de crise (Bortoluzzo, Venezuela, Bortoluzzo, & Nakamura, 2016; Ribeiro, Barbosa, Fonseca, & Frega, 2014) empregam modelos de apreçamento de ativos incondicionais. Além disso, este estudo é o único a analisar os efeitos da crise de 2014 a 2016, que tem características bastante peculiares, uma vez que foi gerada internamente. Finalmente, este estudo deve ter implicações importantes para investidores e empresas em termos de gerenciamento de risco.

Este artigo está organizado da seguinte forma: na próxima seção, é feita uma breve revisão da literatura relacionada aos modelos CAPM incondicional e condicional, além dos estudos que tratam dos efeitos de crises sobre o risco de mercado dos ativos. Na terceira seção, é apresentada a metodologia adotada neste estudo, buscando-se destacar a diferença entre as abordagens do CAPM incondicional e condicional e apresentar os detalhes dos modelos estimados e as formas de estimação. Os resultados empíricos são apresentados na quarta seção e, em seguida, trazem-se algumas considerações finais.

2 REVISÃO DE LITERATURA

O modelo desenvolvido por Lintner (1965), Mossin (1966) e Sharpe (1964), com posteriores contribuições que resultaram na atual versão incondicional do CAPM, é ainda bastante utilizado em finanças para o apreçamento e avaliação de risco de ativos e carteiras, bem como para determinar o custo de capital das empresas. Sua ampla utilização deve-se ao fato de o modelo oferecer boas previsões, além de sua fácil aplicabilidade e interpretação. A versão tradicional do CAPM assume uma estática intertemporal do risco sistemático dos ativos, ou seja, o valor do coeficiente beta de mercado não muda ao longo do tempo, como em Black, Jensen, e Scholes (1972), Blume e Friend (1973) e Fama e MacBeth (1973), e também assume que o retorno e o risco sistemático dos ativos não possuem relações de dependência condicional a variáveis exógenas.

A partir da década de 1970, surgiram diversos trabalhos que tinham como objetivo testar as premissas desse modelo, o que resultou em contribuições apontando falhas do modelo em explicar algumas evidências empíricas. Fama e French (1992), por exemplo, após testarem o CAPM para ações negociadas na NYSE (bolsa de valores de Nova Iorque) entre 1941 e 1990, constataram que a premissa de que o beta do mercado possui uma relação positiva com o retorno esperado das ações não era corroborada para aquele conjunto de dados, sugerindo que outras variáveis poderiam explicar os retornos esperados desses ativos. Além disso, ao contrário do que é previsto pelo CAPM, foi constatado que, em média, empresas menores apresentam retornos maiores, como apontado por Fama e French (1992) e Hansen e Jagannathan (1994).

Alguns padrões observados nos retornos de ações que não eram explicados pelo CAPM passaram a ser considerados anomalias. Buscando explicar essas chamadas anomalias, ao longo do tempo os trabalhos passaram a incorporar novos fatores de risco (modelos multifatores) ou, ainda, considerando apenas o risco de mercado, passaram a incorporar dinâmica no comportamento do beta de mercado. A premissa de que os betas dos ativos se mantêm constantes ao longo do tempo é o fator mais problemático do modelo CAPM tradicional, visto que é mais coerente que o risco relativo de fluxo de caixa de uma firma varie ao longo do ciclo econômico. Em períodos de recessão, por exemplo, a alavancagem de empresas em más condições financeiras pode aumentar em relação a outras firmas, elevando o beta das ações. Dessa forma, os betas e os retornos esperados dependem do conjunto de informações disponíveis, variando ao longo do tempo (Jagannathan & Wang, 1996).

A variabilidade temporal de beta pode ser capturada por meio de um modelo CAPM condicional. Levando-se em conta a dependência de beta com relação ao conjunto de informações disponíveis, trabalhos como os de Avramov e Chordia (2006), Ferson e Harvey (1989), Jagannathan e Wang (1996) e Lettau e Ludvigson (2001) assumem que a dinâmica de beta é uma função de variáveis defasadas relacionadas ao ciclo econômico, como o default spread (ou risco de crédito) e o term spread (ou risco de prazo). De modo geral, essas modelagens mostram resultados mais consistentes do que o modelo CAPM incondicional, reduzindo as anomalias.

Alguns modelos CAPM condicionais obtêm a dinâmica de beta utilizando modelos de séries temporais, como é o caso de Bollerslev, Engle, e Wooldridge (1988), que capturam beta indiretamente, por meio de modelos de volatilidade condicional, e de Faff, Hillier, e Hillier (2000) e Mergner e Bulla (2008), que obtêm beta especificando sua evolução por meio de um processo estocástico.

Em Adrian e Franzoni (2009), é proposto um modelo condicional híbrido para capturar a dinâmica de beta, combinando um processo estocástico de reversão à média e variáveis condicionantes relacionadas ao ciclo econômico. Para estimar a dinâmica de beta, foi utilizado o Filtro de Kalman e, como variáveis condicionantes, os autores adotaram uma variável que sintetiza a razão consumo-riqueza agregada, chamada cay, além do retorno da carteira de mercado, o term spread e o value spread para o mercado norte-americano. Foram encontradas evidências de que o modelo proposto tem desempenho superior ao dos modelos CAPM condicionais baseados apenas nas variáveis relativas ao ciclo econômico e, ainda, reduz significativamente os erros de apreçamento com relação ao CAPM incondicional.

Buscando explorar esses ganhos da modelagem híbrida encontrados para dados do mercado norte-americano, Blank et al. (2014) estimaram o modelo proposto por Adrian e Franzoni (2009) para dados do mercado brasileiro no período de julho de 1999 a maio de 2013. Além do processo estocástico de reversão à média, consideraram, alternativamente, a possibilidade de beta seguir um passeio aleatório. Além das variáveis condicionantes adotadas por Adrian e Franzoni, consideraram também variáveis macroeconômicas relacionadas diretamente à economia brasileira. O modelo que resultou na maior redução dos erros de apreçamento foi a combinação do passeio aleatório com variáveis condicionantes.

Com o intuito de capturar os impactos de crises sobre o risco de mercado (ou beta de mercado) das empresas, estudos empíricos têm empregado o modelo CAPM em suas diferentes versões e, em particular, em sua versão condicional.

Maroney, Naka, & Wansi (2004) analisaram o impacto da crise financeira asiática de 1997 nos betas de seis mercados asiáticos, utilizando o modelo International Capital Asset Pricing Model (ICAPM). Os resultados indicaram que houve aumento nos betas e queda nos retornos médios após o início da crise.

Rahman (2010) empregou um modelo multifator do CAPM para testar a exposição ao risco de bancos comerciais da Malásia no período de 1994 a 2006, abrangendo a crise financeira asiática. Os resultados mostraram que os bancos analisados tiveram maior exposição ao risco durante o período da crise.

Para estimar o custo de capital de bancos com sedes em seis países (Canadá, França, Alemanha, Japão, Reino Unido e Estados Unidos) para o período de 1990 a 2009, King (2009) utilizou o modelo CAPM incondicional. Para cada país, o autor estimou o modelo em três períodos de tempo distintos: o primeiro de 1990 a 2000, o segundo de 2001 a 2005 e o terceiro de 2006 a 2009. Os betas do setor bancário de todos os países da amostra tiveram queda no período de 2001 a 2005, em comparação com o período de 1990 a 2000, com exceção do beta do setor bancário do Japão, que apresentou aumento. Para 2006 a 2009, período que abrange a crise do subprime, o setor bancário do Reino Unido foi o único que apresentou redução no coeficiente beta, enquanto os coeficientes para Estados Unidos, Alemanha e Canadá permaneceram os mesmos e para os demais países da amostra houve um aumento do coeficiente. Pôde-se constatar que o único país em que o setor bancário conseguiu reduzir seu risco ao longo dos três períodos foi o Reino Unido.

Choudhry et al. (2010) investigaram se a crise asiática de 1997 teve algum efeito sobre o beta tempo-variante de quatro setores industriais selecionados da Coreia do Sul, Indonésia, Singapura e Taiwan. Utilizando dados diários de 1 de janeiro de 1992 a 30 de dezembro de 2002, obtiveram os betas tempo-variantes por meio do modelo GARCH BEKK bivariado. Os resultados mostraram que, durante o período de crise (1997 a 1998), houve um aumento substancial no efeito positivo da volatilidade condicional dos retornos da indústria sobre os betas tempo-variantes. Também foi encontrada alguma evidência de aumento no efeito durante o período pós-crise. Choudhry (2005) já havia utilizado a mesma metodologia para analisar os efeitos da crise asiática sobre os betas de mercado de 10 firmas malaias e 10 firmas taiwanesas, e também havia encontrado evidências de aumento nos betas de tais companhias durante o período de crise.

Alexandridis e Hasan (2019) utilizaram um conjunto de dados dos valores diários dos índices de ações de oito mercados europeus, além dos preços das ações que constituem cada índice, para investigar o impacto da crise financeira global e da crise da zona do euro no risco sistemático e no risco de mercado. Os autores dividiram sua amostra em quatro subperíodos, pré-crise (6/2005—7/2007), crise financeira global (8/2007—11/2009), crise da zona do euro (11/2009—12/2013) e pós-crise (1/2014—8/2018), e utilizaram o modelo CAPM com uma abordagem de wavelets para estimar a dinâmica de beta. Os mercados selecionados foram divididos em dois grupos: aquele constituído por países cujas economias, no momento, apresentavam maiores incertezas (Portugal, Itália, Grécia e Espanha) e aquele com economias mais sólidas (Alemanha, Países Baixos, Reino Unido e França). Durante a crise global, os betas aumentaram na França, Alemanha e Portugal, com redução nos demais países. Durante a crise da zona do euro houve aumento nos betas da maioria dos mercados, sendo que os países com economia sólida apresentaram betas em cerca de 1,00 e os demais, em aproximadamente 0,85. No pós-crise, um aumento de beta foi observado na Grécia, Espanha e Portugal, enquanto houve uma ligeira queda nos betas dos demais países.

Para o mercado brasileiro, Ribeiro et al. (2014) analisaram um conjunto de ativos de 31 empresas que compunham o índice Bovespa, classificadas em 14 diferentes setores, para o período de janeiro de 2005 a dezembro de 2011. Foram calculados os betas mensais das empresas para dois intervalos de tempo, o primeiro entre janeiro de 2005 e dezembro de 2007 (pré-crise), e o segundo entre janeiro de 2009 e dezembro de 2011 (pós-crise), com o objetivo de neutralizar o ano de 2008, no qual ocorreu a crise do subprime. Foi utilizado o teste de Kruskal-Wallis para testar se a crise afetou ou não o risco das empresas que constituíam o índice Bovespa. Os autores concluíram que houve uma redução nos betas estimados das empresas para o período pós-crise. Nota-se que essa evidência empírica contraria os resultados de estudos para mercados de outros países.

Bortoluzzo et al. (2016) analisaram os efeitos da crise de 2008 sobre os resultados do modelo CAPM, do modelo de três fatores, de Fama e French, e do modelo de quatro fatores, de Carhart, para dados do mercado brasileiro no período de 2002 a 2013. Foram utilizados dados das ações negociadas na Bolsa de Valores, Mercadorias e Futuros de São Paulo (BM&FBovespa) com periodicidade mensal, excluídas ações do setor financeiro, com patrimônio líquido negativo e sem cotações mensais consecutivas, e foram formadas 13 carteiras de acordo com o índice book-to-market (BM). O período de 2002 a 2013 foi dividido em três—pré-crise, crise e pós-crise—e para o primeiro e o último desses subperíodos foram estimados os modelos uni e multifatoriais não condicionais, e os resultados foram comparados de forma descritiva e por meio do teste de estabilidade dos parâmetros de Chow. Os resultados mostraram um aumento dos betas no período de crise. Contudo, no período pós-crise, cerca de 58% das carteiras apresentaram redução nos betas para os modelos unifatorial e de três fatores, enquanto no modelo de quatro fatores houve redução nos betas de 75% das carteiras, resultados em linha com os obtidos por Ribeiro et al. (2014).

2.1 O MODELO CAPM

Proposto por Lintner (1965), Mossin (1966) e Sharpe (1964), o Capital Asset Pricing Model (CAPM) é o modelo mais conhecido em finanças para analisar a relação de risco-retorno de ativos financeiros. O modelo sugere que o retorno esperado de um ativo ou carteira, 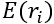é igual à taxa de juros livre de risco, 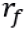, mais o prêmio pelo risco:

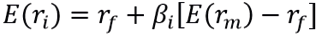(1)

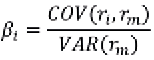(2)

Em que o prêmio pelo risco é dado pela multiplicação do coeficiente beta, 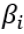, pela diferença entre o retorno esperado da carteira de mercado, 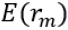, e pela taxa de juros livre de risco.

Econometricamente, essa relação costuma ser estimada em termos de excesso de retorno. A suposição, nesse caso, é de que os retornos históricos são uma boa proxy para os retornos esperados e de que os retornos excedentes possuem distribuição normal 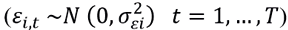. A equação estimada por mínimos quadrados ordinários (MQO) é definida por:

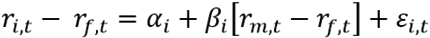(3)

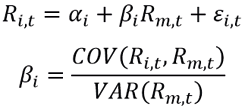(4)

Nesse caso, o beta é o coeficiente de inclinação dessa regressão. O coeficiente 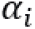, conhecido como “Alfa de Jensen”, é o intercepto da equação e mostra o excesso de retorno do ativo. Se a hipótese de mercados eficientes for atendida, o Alfa de Jensen será estatisticamente igual a zero.

Em geral, os agentes no mercado financeiro são avessos ao risco, por esse motivo, normalmente exigem um prêmio pelo risco, que tende a ser maior para investimentos mais arriscados. São considerados essencialmente dois tipos de risco aos quais os ativos financeiros estão submetidos, descritos por Ross, Westerfield, Jordan, e Lamb (2013):

risco sistemático: também conhecido como risco de mercado, ou risco não diversificável, é aquele que influencia de forma ampla um grande número de ativos;
risco não sistemático: também conhecido como risco diversificável, é o risco que atinge um único ativo ou um grupo pequeno de ativos e que pode ser reduzido por meio da diversificação da carteira.

Como o risco não sistemático pode ser eliminado facilmente mediante a diversificação, o cálculo do retorno esperado e do prêmio pelo risco de um ativo ou carteira depende apenas do risco sistemático, medido pelo coeficiente beta, 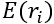. Portanto, se 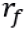, o risco é menor que o da carteira de mercado; se 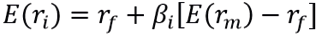, o risco é igual ao da carteira de mercado; se 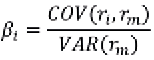, o risco é maior que o da carteira de mercado; e se 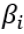, o ativo ou carteira segue uma tendência contrária à carteira de mercado.

2.2 MODELO CAPM CONDICIONAL

Diferentemente do CAPM incondicional, o CAPM condicional permite que os betas e prêmios de risco variem ao longo do tempo, de acordo com o ciclo econômico, podendo ser escrito como:

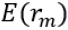(5)

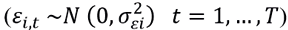(6)

De acordo com a Equação 5, 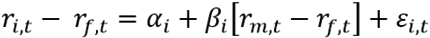é o beta condicional do ativo i e os valores esperados do excesso de retorno do ativo i e do excesso de retorno da carteira de mercado em t+1 estão condicionados ao conjunto de informações disponíveis no período anterior, .

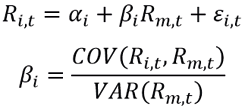A literatura empírica geralmente usa variáveis condicionantes relacionadas ao ciclo econômico como proxy para a informação disponível aos investidores no período t, como o default spread (ou risco de crédito), o term spread (ou risco de prazo), a inflação, a taxa de câmbio, o rendimento de dividendos, entre outros. A premissa é de que o risco associado aos fluxos de caixa das empresas pode variar de acordo com o ciclo econômico, em momentos de recessão ou expansão da economia.

Além do uso de variáveis condicionantes, o CAPM condicional ainda permite especificar a dinâmica de beta a partir de modelos de séries temporais.

3 METODOLOGIA

No presente artigo, com base em um modelo de espaço-estado, como em Blank et al. (2014), modelou-se a dinâmica de beta como um processo estocástico (de reversão à média ou passeio aleatório), incluindo ou não um conjunto de variáveis condicionantes relacionadas aos ciclos econômicos. O modelo é descrito a seguir:

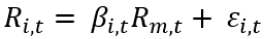
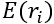(7)

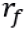
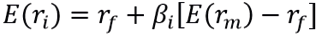(8)

Em que 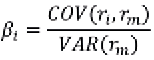é a média de longo prazo de 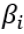é o parâmetro de persistência da dinâmica de beta, que revela a força de reversão do processo para sua média incondicional, 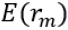é o vetor de variáveis explicativas defasadas relacionadas ao ciclo econômico, e 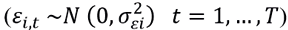, é o vetor de coeficientes que relaciona 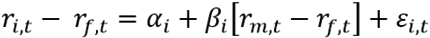com .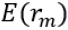

Se 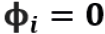, beta segue um processo de reversão à média e, ainda, se 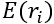, beta segue um passeio aleatório. Neste estudo, assim como em Blank et al. (2014), serão considerados dois processos estocásticos para a modelagem de beta:

Beta como passeio aleatório (PA):
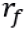
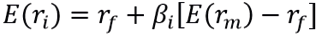(9)
Beta como reversão à média (RM):

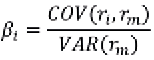
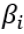(10)

A dinâmica de beta é estimada por meio do Filtro de Kalman.

Alternativamente, considerando qu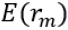e e 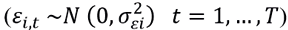na Equação 8, tem-se o modelo tradicional do CAPM condicional, em que beta é uma função determinística de variáveis condicionantes:

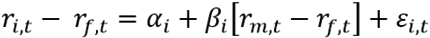(11)

Substituindo (11) na Equação 7, tem-se um modelo de múltiplos fatores, que pode ser estimado por mínimos quadrados ordinários:

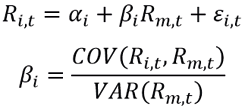(12)

Assim como Blank et al. (2014), estimou-se por MQO o modelo dado pela Equação 12 com a finalidade de verificar a capacidade de as variáveis condicionantes explicarem a dinâmica de beta. Em seguida, estimaram-se modelos em que beta é descrito por um processo estocástico (passeio aleatório ou reversão à média) com e sem a inclusão das variáveis condicionantes. Para efeitos comparativos, também se estimou o beta estático do modelo incondicional.

3.1 FILTRO DE KALMAN

Para estimar os modelos com coeficientes variantes no tempo (Durbin & Koopman, 2001), usou-se um modelo na forma espaço-estado que pode ser descrito a partir das suas equações de observação e de estado:

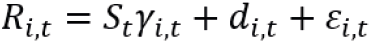
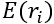(13)

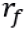
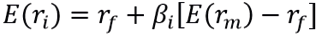(14)

Em qu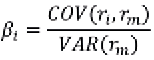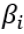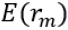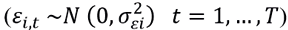e ; ; ; ; e 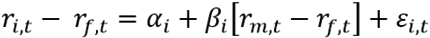para todo .

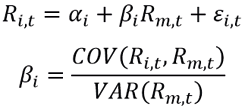O modelo dado pelas Equações 7 e 8 pode ser escrito considerando a média de longo prazo como uma variável de estado a ser estimada a cada nova observação. Neste artigo, assim como em Blank et al. (2014), a média de longo prazo é tratada como desconhecida pelos investidores, portanto, apesar de considerada constante na definição do processo, é modelada como uma variável de estado, tendo seu valor atualizado a cada nova observação. Na forma matricial tem-se:

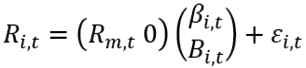
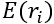(15)

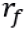
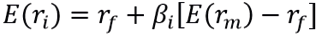(16)

Adequando às Equações 13 e 14, tem-se:

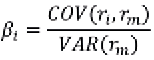(17)

Sejam

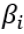(18)

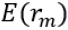(19)

Em que 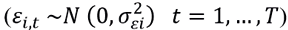. Por meio do Filtro de Kalman, pode-se estimar recursivamente o vetor de estado, combinando o passo de atualização e previsão do filtro.

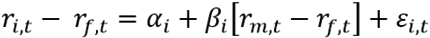(20)

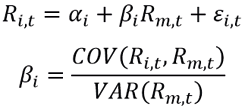(21)

Em que ; ; ; ; .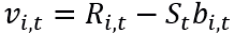

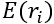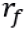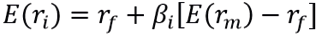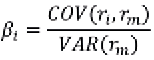O conjunto de hiperparâmetros 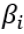para cada ativo 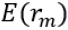é dado pelos parâmetros 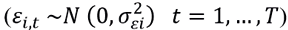, , 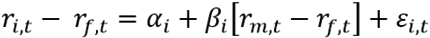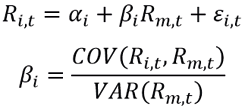e , e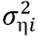stimados por máxima verossimilhança. A função de log-verossimilhança é dada por

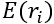(22)

Em que .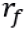

3.2 DADOS

Para a estimação dos modelos propostos, utilizaram-se os retornos de uma carteira composta por 10 ações de empresas brasileiras negociadas na B3, calculados a partir dos preços de fechamento ajustados dos ativos; os retornos da carteira de mercado, calculados a partir dos valores de fechamento do Ibovespa; e, como retornos do ativo livre de risco, utilizou-se a taxa efetiva do CDI. Como variáveis condicionantes, utilizaram-se quatro variáveis relacionadas aos ciclos econômicos: o term spread, calculado como a diferença entre os retornos dos contratos de swap de juros de 360 dias e de 180 dias; a variação da taxa de câmbio, calculada pelo preço de fechamento do dólar PTAX; o retorno da carteira de mercado; e a taxa de inflação, dada pela variação do IPCA.

Os dados têm periodicidade mensal e abrangem o período de fevereiro de 2010 a dezembro de 2018. Com exceção das variáveis para o cálculo do term spread, que foram coletadas a partir do Ipeadata (2019), todas as demais variáveis foram coletadas a partir da base de dados Economática® (2019). Os dez ativos que compõem a carteira estão listados na Tabela 1. As ações foram escolhidas de acordo com a carteira teórica do Ibovespa do dia 4 de dezembro de 2018 e de acordo com a disponibilidade de dados para o período estudado. A carteira foi construída de modo a ter dez setores distintos, seguindo a classificação da B3. Dentro de cada setor, foi escolhida a ação com o maior peso na composição do índice. Buscou-se construir uma carteira em que diferentes setores da economia estivessem representados, dada a exposição heterogênea dos setores aos ciclos econômicos.

Tabela 1

Carteira de ações

Empresa	Código de negociação	Setor	Participação na carteira
Itaú Unibanco	ITUB4	Bancos	10%
Vale	VALE3	Mineração	10%
Petrobras	PETR4	Petróleo, gás e biocombustíveis	10%
Ambev	ABEV3	Bebidas	10%
B3	B3SA3	Serviços financeiros diversos	10%
Lojas Renner	LREN3	Comércio	10%
Telefônica	VIVT4	Telecomunicação	10%
JBS	JBSS3	Alimentos processados	10%
Embraer	EMBR3	Materiais de transporte	10%
Gerdau	GGBR4	Siderurgia e metalurgia	10%

Foi testada a estacionariedade das séries utilizadas nos modelos empíricos por meio dos testes de Dickey-Fuller Aumentado (ADF), Phillips–Perron (PP) e Kwiatkowski-Philips-Schmidt-Shin (KPSS). Como mostra a Tabela 2, os testes indicam que todas as séries são estacionárias em nível:

Tabela 2

Resultados dos testes de raiz unitária

	Em nível			Primeira diferença
Variáveis	ADFA	PPB	KPSSC	ADF	PP	KPSS
Carteira	-8,58***	-9,52***	0,17	-8,10***	-59,15***	0,13
IBOV	-9,56***	-9,60***	0,33	-13,30***	-47,66***	0,15
Dólar PTAX	-11,19***	-11,16***	0,11	-8,68***	-105,13***	0,16
Inflação	-5,06***	-5,18***	0,23	-10,17***	13,62***	0,03
Term spread	-2,92**	-2,57	0,22	-7,28***	-7,23***	0,18

Nota. *, **, *** denotam rejeição da hipótese nula do teste a, respectivamente, 10%, 5% e 1% de níveis de significância. Testes aplicados para equações com constante e sem tendência. A: Foi utilizado o método de Schwarz. B: Foi utilizado o método Bartlett Kernel com Newey-West Bandwidth. C: O teste KPSS tem hipótese nula de estacionariedade. Foi utilizado o método Bartlett Kernel com Newey-West Bandwidth.

4 RESULTADOS EMPÍRICOS

Os resultados da estimação do CAPM incondicional, apresentados na Tabela 3, mostram um alfa de Jensen não significativo ao nível de 5%, assim como esperado pela teoria, e um beta estatisticamente significativo. O valor da estimativa de beta, 0,87, sugere que a carteira construída é menos arriscada do que a carteira de mercado. Os testes de diagnósticos sobre os resíduos (normalidade, autocorrelação e heterocedasticidade) sugerem que o modelo está corretamente ajustado.

Tabela 3

Estimativas do CAPM incondicional

Coeficientes		Diagnósticos sobre os resíduos
α	β	JB	Q(12)	Q²(12)
0,36*	0,87***	0,44	14,46	11,32

Nota. *, **, *** denotam rejeição da hipótese nula do teste a, respectivamente, 10%, 5% e 1% de significância. JB é a estatística de Jarque-Bera, com hipótese nula de normalidade dos resíduos. Q(12) é a estatística de Ljung-Box do teste da hipótese nula de não autocorrelação nos resíduos até a defasagem de ordem 12. Q²(12) é a estatística de Ljung-Box do teste da hipótese nula de não autocorrelação nos resíduos ao quadrado até a defasagem de ordem 12.

Os resultados obtidos a partir da estimação do modelo em que beta é uma função determinística das variáveis condicionantes, dado pela Equação 12, são encontrados na Tabela 4. Apenas o coeficiente relacionado ao term spread é estatisticamente significativo, no entanto, por meio da estatística F do teste de Wald, realizado para as variáveis condicionantes em conjunto, verifica-se que o conjunto das variáveis do vetor é significativo. O modelo também obteve bons resultados nos testes de diagnósticos sobre os resíduos.

Tabela 4

Estimativas do modelo considerando beta como função das variáveis condicionantes

Coeficientes					F-statistic	Diagnósticos sobre os resíduos
φ0	φRm	φPTAX	φterm	φIPCA	φ›Z	JB	Q(12)	Q²(12)
0,86***	0,003	-0,01	-0,15**	0,18	3,25**	0,92	14,88	6,04

Historicamente, o term spread foi capaz de antecipar recessões. Nos períodos pós-guerra, todas as vezes que o term spread ficou negativo, uma recessão aconteceu em seguida (Estrella & Hardouvelis, 1991; Harvey, 1989). Esse movimento sinaliza que o mercado enxerga maior risco de crédito no curto prazo do que no longo prazo. O coeficiente negativo do term spread apresentado na Tabela 4, portanto, indica que o beta da carteira tende a aumentar em períodos em que o mercado espera uma recessão.

Dada a significância conjunta do vetor , estimaram-se as equações do CAPM condicional em que beta é descrito como um processo estocástico (passeio aleatório ou reversão à média) com e sem a inclusão de variáveis condicionantes, utilizando o Filtro de Kalman. Os resultados podem ser vistos na Tabela 5. Todos os quatro modelos apresentam resultados satisfatórios para os testes de diagnósticos sobre os resíduos. A variância do erro da equação de estado não se mostrou estatisticamente significativa no modelo em que o beta é uma combinação de passeio aleatório e função das variáveis condicionantes (PA + variáveis). No modelo em que o beta combina a reversão à media com variáveis condicionantes (RM + variáveis), os coeficientes das variáveis condicionantes não se mostraram significativos. Em decorrência disso, as dinâmicas dos betas desses dois modelos não foram apresentadas na Figura 1. Nos modelos em que o beta é apenas um processo estocástico (passeio aleatório (PA) e reversão à média (RM)) todos os coeficientes são significativos.

Tabela 5

Estatísticas do CAPM condicional

Modelo	PA	PA + variáveis	RM	RM + variáveis
Coeficientes
σ²ε	3,02***	3,02***	2,69***	2,84***
σ²η	0,002***	4,7E-13	0,02***	0,01***
Bi	–	–	0,87***	0,86***
δ	–	–	0,59***	0,47**
φRm	–	0,001	–	-0,01
φPTAX	–	0,005	–	-0,01
φterm	–	0,007	–	-0,03
φIPCA	–	0,017	–	0,12
Diagnósticos sobre os resíduos
JB	0,82	0,50	1,71	1,23
Q(12)	13,08	9,50	14,91	14,63
Q²(12)	9,37	8,44	14,60	14,64

Nota. *, **, *** denotam rejeição da hipótese nula do teste a, respectivamente, 10%, 5% e 1% de significância. JB é a estatística de Jarque-Bera, com hipótese nula de normalidade dos resíduos. Q(12) é a estatística de Ljung-Box para a hipótese nula de não autocorrelação nos resíduos até a defasagem de ordem 12. Q²(12) é a estatísitca de Ljung-Box para a hipótese nula de não autocorrelação nos resíduos ao quadrado até a defasagem de ordem 12.

A Figura 1 compara as trajetórias temporais de beta obtidas com base no CAPM condicional com o beta estimado pelo CAPM incondicional (beta constante ao longo do tempo). Pode-se observar, na Figura a seguir, que o beta de mercado da carteira construída oscilou acerca do valor de beta estimado pelo modelo incondicional (0,87) até final de 2014, quando, então, teve um aumento a partir de janeiro de 2015, ficando acima do valor obtido a partir do modelo estático, e somente retornou a valores próximos do período pré-crise a partir de março de 2018.

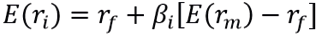
Figura 1. Betas estimados pelo CAPM condicional e pelo CAPM incondicional.

As trajetórias de beta obtidas neste artigo para o período da crise econômica no Brasil de 2014 a 2016 seguem os resultados da maior parte dos estudos empíricos internacionais que analisam o impacto de crises sobre o risco sistemático de ativos financeiros, os quais mostram que o beta de mercado tende a aumentar nos períodos de crise (Alexandridis e Hasan, 2019; Asgharian et al., 2017; Choudhry, 2005; Choudhry et al., 2010; Maroney et al., 2004; Rahman, 2010) e pós-crise (Alexandridis e Hasan, 2019; Choudhry et al., 2010). Esses resultados mostram que a posição de risco das firmas é sensível ao estado da economia. O aumento na magnitude de beta reflete a sensibilidade do mercado financeiro às variáveis financeiras e econômicas.

Os resultados deste estudo empírico, entretanto, vão de encontro aos resultados observados em Bortoluzzo et al. (2016) e Ribeiro et al. (2014), que analisaram os impactos da crise do subprime sobre os betas de mercado das empresas brasileiras e encontraram evidências de redução no risco de mercado no período pós-crise. Vale destacar, no entanto, que a crise do subprime e a crise econômica de 2014 a 2016 no Brasil têm características bastante distintas e os cenários conjunturais de cada época podem ter contribuído para os resultados divergentes. A crise de 2008 teve origem no mercado financeiro internacional e, na época, o Governo brasileiro adotou uma série de estímulos à economia, visando aumentar o consumo, o que suavizou os efeitos da crise no País. Por sua vez, a crise de 2014 a 2016 teve origem interna, sendo o resultado de um conjunto de choques de oferta e de demanda (Barbosa, 2017), com o Governo enfrentando um forte desequilíbrio fiscal em razão de políticas expansionistas desfavoráveis, e uma crise política que culminou no impeachment da então Presidente Dilma Rousseff e, ainda, em meio a escândalos de corrupção, o que fragilizou a confiança dos investidores. Nesse cenário, os estímulos governamentais à economia já não funcionavam, não sendo capazes de melhorar o ânimo dos investidores, o que pode justificar o aumento dos betas no mercado financeiro durante o período. Vale destacar, ainda, que, apesar de o País ter saído do quadro de recessão e da mudança de governo após o impeachment de Dilma Rousseff, o ano de 2017 ainda foi marcado pela crise política e pelo forte déficit nas contas públicas e, inclusive, por escândalos envolvendo o então Presidente Michel Temer, o que pode explicar a persistência de beta acima do nível pré-crise.

5 CONSIDERAÇÕES FINAIS

Este estudo teve por objetivo investigar os efeitos da crise econômica de 2014 a 2016 sobre o risco sistemático dos ativos do mercado de capitais brasileiro. Para isso, analisou-se o comportamento do beta de mercado de uma carteira composta por 10 ações negociadas na B3, no período de fevereiro de 2010 a dezembro de 2018, por meio da estimação de um modelo CAPM condicional em que a dinâmica de beta é dada por um processo estocástico combinado com variáveis relacionadas ao ciclo econômico. Para efeito de comparação, também se estimou um modelo em que beta é uma função determinística de variáveis condicionantes relacionadas ao ciclo econômico, além do CAPM incondicional.

As trajetórias de beta obtidas a partir dos modelos condicionais selecionados mostraram uma elevação desse coeficiente a partir de 2015, período em que a crise política e fiscal já se encontrava instaurada no País, e este somente voltou a patamares pré-crise no final do primeiro trimestre de 2018. O risco sistemático da carteira manteve-se elevado não apenas durante o período de crise (2015 a 2016), mas também durante todo o ano de 2017 e início de 2018. É importante destacar que, apesar de o País ter saído da recessão no início de 2017, este ano ainda foi marcado pela crise política e pelo déficit nas contas públicas.

Ao contrário do comportamento do beta do mercado brasileiro durante a crise do subprime apresentado nos estudos de Bortoluzzo et al. (2016) e Ribeiro et al. (2014), o comportamento de beta encontrado neste artigo está de acordo com o esperado, dadas as evidências encontradas na literatura internacional de que o coeficiente beta tende a aumentar em períodos durante e pós-crise, em razão da volatilidade gerada pelo ambiente de incertezas. É possível, nesse caso, que as diferenças entre a crise financeira global de 2008 e a crise de 2014 a 2016 expliquem os resultados distintos deste estudo em relação aos estudos de Bortoluzzo et al. (2016) e Ribeiro et al. (2014), além do fato de estes não modelarem a dinâmica de beta por meio de um modelo de apreçamento condicional.

Este estudo contribui, então, para a literatura escassa que trata dos efeitos de crises sobre o risco de mercado de ativos negociados no mercado de capitais brasileiro, trazendo novas evidências empíricas, contrárias às evidências de estudos anteriores para o caso brasileiro, mas de acordo com a literatura internacional, além de analisar os efeitos, até então não estudados, da crise de 2014 a 2016, com suas características singulares. Também traz importantes implicações em termos de gerenciamento de risco: dadas as evidências de aumento no risco sistemático das ações das empresas negociadas na B3 em decorrência do aumento na volatilidade durante o período de crise, os investidores tendem, então, a demandar retornos mais elevados ou a migrar para ativos menos arriscados. Isso acaba aumentando o custo de financiamento das empresas de capital aberto e reduzindo o investimento em um período no qual ele é tão necessário.

Como trabalho futuro, seria importante aumentar esta amostra de dados e verificar se os resultados se mantêm, visto que uma das limitações do estudo é o tamanho restrito da carteira estudada. Seria interessante, também, estender a análise para investigar os efeitos de outras crises, como a do subprime e a da dívida soberana dos países da zona do euro, utilizando o modelo CAPM híbrido.

Agradecimentos

Vinícius Luís de Souza Nonato agradece o apoio financeiro do CNPq (PIBIC/CNPq— 20/2017) durante a realização deste trabalho. Paula Virgínia Tófoli agradece o apoio financeiro da Fundação de Apoio à Pesquisa do Distrito Federal (FAPDF) (Processo SEI n. 00193—00000004/2019-50).

Referências

Adrian, T., & Franzoni, F. (2009). Learning about beta: Time-varying factor loadings, expected returns, and the conditional CAPM. Journal of Empirical Finance, 16(4), 537-556.

Alexandridis, A. K., & Hasan, M. S. (2019). Global financial crisis and multiscale systematic risk: Evidence from selected European stock markets. International Journal of Finance & Economics, 1-29. doi:10.1002/ijfe.1764

Asgharian, H., Christiansen, C., & Hou, A. J. (2017). Long-run and short-run components of factor betas: Implications for equity pricing. Sardenha, Itália: World Finance Program Meeting.

Avramov, D., & Chordia, T. (2006). Asset Pricing Models and Financial Market Anomalies. The Review of Financial Studies, 19(3), 1001-1040.

Barbosa, F. H. (2015). Crises econômicas e política de 2015: Origens e consequências. Revista de Conjuntura Econômica, 69(9), 53.

Barbosa, F. H., Filho. (2017). A crise econômica de 2014/2017. Estudos Avançados, 31(89), 51-60.

Black, F., Jensen, M., & Scholes, M. (1972). The capital asset pricing model: Some empirical tests. In M. Jensen (Ed.), Studies in the theory of capital markets. New York: Praeger.

Blank, F. F., Samanez, C. P., Baidya, T. K. N., & Aiube, F. A. L. (2014). CAPM Condicional: Betas Variantes no Tempo no Mercado Brasileiro. Brazilian Review of Finance, 12(2) 163-199.

Blume, M., & Friend, I. (1973). A new look at capital asset pricing model. Journal of Finance, 28(1), 19-33.

Bollerslev, T., Engle, R. F., & Wooldridge, J. M. (1988). A Capital Asset Pricing Model with Time-Varying Covariances. Journal of Political Economy, 96(1), 116-131.

Bortoluzzo, A. B., Venezuela, M. K., Bortoluzzo, M. M., & Nakamura, W. T. (2016). Influência da crise financeira de 2008 na previsibilidade dos modelos de apreçamento de ativos de risco no Brasil. Revista Contabilidade & Finanças, 27(72), 408-420.

Chen, C., & So, R. (2002). Exchange rate variability and the riskiness of US multinational firms: evidence from the Asian financial turmoil. Journal of Multinational Financial Management, 12, 411-428.

Choudhry, T., Lu, L., & Peng, K. (2010). Time-varying beta and the Asian financial crisis: Evidence from the Asian industrial sectors. Japan and the World Economy, 22, 228-234.

Choudhry, T. (2005). Time-varying beta and the Asian financial crisis: Evidence from Malaysian and Taiwanese firms. Pacific-Basin Finance Journal, 3, 93-118.

Durbin, J., & Koopman, S. J. (2001). Time Series Analysis by State Space Methods. Oxford: Oxford University Press.

Economatica. (2019). Recuperado de https://economatica.com

Estrella, A., & Hardouvelis, G. (1991). The term structure as a predictor of real economic activity. Journal of Finance, 46(2), 555-576.

Fabozzi, F., & Francis, J. (1978). Beta as a random coefficient. Journal of Financial and Quantitative Analysis, 13, 101-116.

Faff, R. W., Hillier, D., & Hillier, J. (2000). Time Varying Beta Risk: An Analysis of Alternative Modelling Techniques. Journal of Business Finance & Accounting, 27(5-6), 523-554.

Fama, E. F., & French, K. R. (2004). The Capital Asset Pricing Model: Theory and Evidence. Journal of Economic Perspectives, 18(3), 25-46.

Fama, E. F., & French, K. R. (1992). The Cross-Section of Expected Stock Returns. The Journal of Finance, 47(2), 427-465.

Fama, E. F., & MacBeth, D. (1973). Risk, return and equilibrium: Empirical test. Journal of Political Economy, 3(81), 607-636.

Ferson, W. E., & Harvey, C. R. (1999). Conditioning Variables and the Cross Section of Stock Returns. The Journal of Finance, 54(4), 1325-1360.

Hansen, L. P., & Jagannathan, R. (1994). Assessing specification errors in stochastic discount factor models. Technical working paper, 153.

Harvey, C. (1989). Time-varying conditional covariances in tests of asset pricing models. Journal of Financial Economics, 24(2), 289-317.

Ipeadata. (2019). Macroeconômico Regional Social. Recuperado de http://ipeadata.gov.br

Jagannathan, R., & Wang, Z. E. (1996). The Conditional CAPM and the Cross-Section of Expected Returns. The Journal of Finance, 51(1), 3-53.

King, M. R. (2009). The cost of equity for global banks: A CAPM perspective from 1990 to 2009. BIS Quarterly Review, 59-73.

Lettau, M., & Ludvigson, S. (2001). Resurrecting the (C)CAPM: A cross-sectional test when risk premia are time-varying. Journal of Political Economy, 109(6), 1238-1287.

Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics, 47(1), 13-37.

Maroney, N., Naka, A., & Wansi, T. (2004). Changing risk, return and leverage: The 1997 Asian financial crisis. Journal of Financial and Quantitative Analysis, 39(1), 143-166.

Mergner, S., & Bulla, J. (2008). Time-varying beta risk of Pan-European industry portfolios: A comparison of alternative modeling techniques. The European Journal of Finance, 14(8), 771-802.

Mossin, J. (1966). Equilibrium in a Capital Asset Market. Econometrica: Journal of the Econometric Society, 34(4), 768-783.

Rahman, A. A. (2010). Three-factor capm risk exposures: Some evidence from Malaysian commercial banks. Asian Academy of Management Journal of Accounting and Finance, 6(1), 47-67.

Ribeiro, F., Barbosa, J. S., Fonseca, M. W., & Frega, J. R. (2014). Impactos da crise financeira de 2008: Um estudo sobre as variações do coeficiente beta no mercado de capitais brasileiro. Revista Capital Científico, 12(1), 27-41.

Ross, S. A., Westerfield, R. W., Jordan, B. D., & Lamb, R. (2013). Fundamentos de administração financeira. (9ª ed.). Porto Alegre: AMGH.

Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19(3), 425- 442.

Como citar este artigo:

ABNT

NONATO; Vinícius Luís de Souza; TÓFOLI, Paula Virgínia. Impacto da crise econômica de 2014 a 2016 sobre o coeficiente beta do mercado de capitais brasileiro. RACE, Revista de Administração, Contabilidade e Economia, Joaçaba: Editora Unoesc, v. 19, n. 3, p. 441-462, maio/ago. 2020. Disponível em: http://editora.unoesc.edu.br/index.php/race. Acesso em: dia/mês/ano.

APA

Nonato, V. L. de S., & Tófoli, P. V. (2020). Impacto da crise econômica de 2014 a 2016 sobre o coeficiente beta do mercado de capitais brasileiro. RACE, Revista de Administração, Contabilidade e Economia, 19(3), 441-462. Recuperado de http://editora.unoesc.edu.br/index.php/race